（本题12分）如图，在平面直角坐标系中，点A（10，0），以-优题课

（本题12分）如图，在平面直角坐标系中，点A（10，0），以OA为直径在第一象限内作半圆C，点B是该半圆周上一动点，连结OB、AB，并延长AB至点D，使DB=AB，过点D作x轴垂线，分别交x轴、直线OB于点E、F，点E为垂足，连结CF．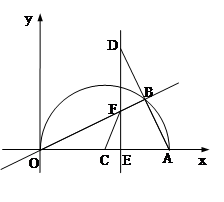

（1）当∠AOB=30°时，求弧AB的长度；
（2）当DE=8时，求线段EF的长；
（3）在点B运动过程中，当交点E在O，C之间时，是否存在以点E、C、F为顶点的三角形与△AOB相
似，若存在，请求出此时点E的坐标；若不存在，请说明理由．

科目数学题型解答题难度未知

图1表示的是某书店今年 $1 ~ 5$ 月的各月营业总额的情况，图2表示的是该书店"党史"类书籍的各月营业额占书店当月营业总额的百分比情况．若该书店 $1 ~ 5$ 月的营业总额一共是182万元，观察图1、图2，解答下列问题：

（1）求该书店4月份的营业总额，并补全条形统计图．

（2）求5月份"党史"类书籍的营业额．

（3）请你判断这5个月中哪个月"党史"类书籍的营业额最高，并说明理由．

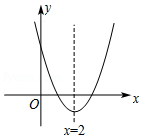
如图，二次函数 $y = (x - 1) (x - a) (a$ 为常数）的图象的对称轴为直线 $x = 2$ ．

（1）求 $a$ 的值．

（2）向下平移该二次函数的图象，使其经过原点，求平移后图象所对应的二次函数的表达式．

如图是由边长为1的小正方形构成的 $6 \times 4$ 的网格，点 $A$ ， $B$ 均在格点上．

（1）在图1中画出以 $AB$ 为边且周长为无理数的 $▱ ABCD$ ，且点 $C$ 和点 $D$ 均在格点上（画出一个即可）．

（2）在图2中画出以 $AB$ 为对角线的正方形 $AEBF$ ，且点 $E$ 和点 $F$ 均在格点上．

（1）计算： $(1 + a) (1 - a) + {(a + 3)}^{2}$ ．

（2）解不等式组： $\{\begin{matrix} 2 x + 1 < 9 \\ 3 - x ⩽ 0 \end{matrix}$ ．

如图，在菱形 $ABCD$ 中， $∠ ABC$ 是锐角， $E$ 是 $BC$ 边上的动点，将射线 $AE$ 绕点 $A$ 按逆时针方向旋转，交直线 $CD$ 于点 $F$ ．

（1）当 $AE ⊥ BC$ ， $∠ EAF = ∠ ABC$ 时，

①求证： $AE = AF$ ；

②连结 $BD$ ， $EF$ ，若 $\frac{EF}{BD} = \frac{2}{5}$ ，求 $\frac{S_{ΔAEF}}{S_{菱形 ABCD}}$ 的值；

（2）当 $∠ EAF = \frac{1}{2} ∠ BAD$ 时，延长 $BC$ 交射线 $AF$ 于点 $M$ ，延长 $DC$ 交射线 $AE$ 于点 $N$ ，连结 $AC$ ， $MN$ ，若 $AB = 4$ ， $AC = 2$ ，则当 $CE$ 为何值时， $ΔAMN$ 是等腰三角形．

试卷网试题网古诗词网作文网范文网