如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
某软件商店经销一种热门益智游戏软件,进货成本为每盘8元,若按每盘10元销售,每天能售出200盘;但由于货源紧缺,商店决定采用尽量提高软件售价减少销售量的办法增加利润,如果这种软件每盘售价提高2元其销售量就减少40盘,问应将每盘售价定为多少元时,才能使每天利润为640元?这时的销售量应为多少?
2014年5月12日,国家统计局公布了《2013年农民工监测调查报告》,报告显示:我国农民工收入持续快速增长.某地区农民工人均月收入增长率如图1,并将人均月收入绘制成如下图的不完整的条形统计图.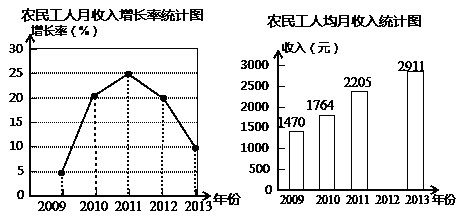
根据以上统计图解答下列问题:
(1)2013年农民工人均月收入的增长率是多少?
(2)2011年农民工人均月收入是多少?
(3)小明看了统计图后说:“农民工2012年的人均月收入比2011年的少了.”你认为小明的说法正确吗?请说明理由.
如图,九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,人的眼睛E、标杆顶点C和旗杆顶点A在同一直线,求旗杆AB的高度.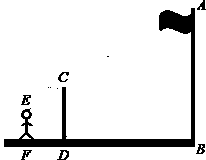
如图,路灯下一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.
(1)指定路灯的位置(用点P表示);
(2)在图中画出表示大树高的线段;
(3)若小明的眼睛近似地看成是点D,试画图分析小明能否看见大树.