如图,点 为圆形纸片内不同于圆心
为圆形纸片内不同于圆心 的定点,动点
的定点,动点 在圆周上,将纸片折起,使点
在圆周上,将纸片折起,使点 与点
与点 重合,设折痕
重合,设折痕 交线段
交线段 于点
于点 .现将圆形纸片放在平面直角坐标系
.现将圆形纸片放在平面直角坐标系 中,设圆
中,设圆 :
: ,记点
,记点 的轨迹为曲线
的轨迹为曲线 .
.
⑴证明曲线 是椭圆,并写出当
是椭圆,并写出当 时该椭圆的标准方程;
时该椭圆的标准方程;
⑵设直线 过点
过点 和椭圆
和椭圆 的上顶点
的上顶点 ,点
,点 关于直线
关于直线 的对称点为点
的对称点为点 ,若椭圆
,若椭圆 的离心率
的离心率 ,求点
,求点 的纵坐标的取值范围.
的纵坐标的取值范围.
某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:,,… ,后得到如图的频率分布直方图.
(1)求图中实数 的值;
的值;
(2)若该校高一年级共有学生500人,试估计该校高一年级在这次考试中成绩不低于60分的人数.
(3)若从样本中数学成绩在与两个分数段内的学生中随机选取两名学生,试用列举法求这两名学生的数学成绩之差的绝对值不大于10的概率.
已知 :
: ,
, :函数
:函数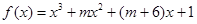 存在极大值和极小值,求使“
存在极大值和极小值,求使“ ”为真命题的实数
”为真命题的实数 的取值范围.
的取值范围.
已知函数 .
.
(1)若 ,解方程
,解方程 ;
;
(2)若函数 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
(3)若 且不等式
且不等式 对一切实数
对一切实数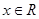 恒成立,求
恒成立,求 的取值范围
的取值范围
已知数列 满足
满足 且
且 。
。
(1)求 的值;
的值;
(2)是否存在一个实数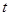 ,使得
,使得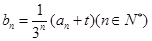 且
且 为等差数列?若存在,求出
为等差数列?若存在,求出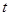 的值;如不存在,请说明理由;
的值;如不存在,请说明理由;
(3)求数列 的前n项和
的前n项和 .
.
已知过抛物线y2=2px(p>0)的焦点,斜率为2的直线交抛物线于A(x1,y1),B(x2,y2)(x1<x2)两点,且|AB|=9.
(1)求该抛物线的方程;
(2)O为坐标原点,C为抛物线上一点,若 ,求λ的值.
,求λ的值.