选修4—5;不等式选讲.设函数 .
.
(Ⅰ)解不等式 ;
;
(Ⅱ)对于实数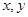 ,若
,若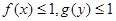 ,求证
,求证 .
.
(本小题满分12分)
已知集合A={a2,a+1,-3},B={a-3,a2+1,2a-1},若A∩B={-3},
(Ⅰ)求实数a的值.
(Ⅱ)设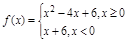 ,求不等式
,求不等式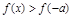 的解集。
的解集。
(本小题满分14分)
设函数 (
( 为实常数)为奇函数,函数
为实常数)为奇函数,函数 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 在
在 上的最大值;
上的最大值;
(Ⅲ)当 时,
时, 对所有的
对所有的 及
及 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知函数 的图象过点
的图象过点 ,且图象上与点P最近的一个最低点是
,且图象上与点P最近的一个最低点是 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若 ,且
,且 为第三象限的角,求
为第三象限的角,求 的值;
的值;
(Ⅲ)若 在区间
在区间 上有零点,求
上有零点,求 的取值范围.
的取值范围.
(本小题满分12分)
设函数 其中
其中 .
.
(Ⅰ)证明: 是
是 上的减函数;
上的减函数;
(Ⅱ)若 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)
已知函数 .
.
(Ⅰ)求函数 的对称轴方程;
的对称轴方程;
(Ⅱ)画出 在区间
在区间 上的图象,并求
上的图象,并求 在
在 上的最大值与最小值.
上的最大值与最小值.