(1)焦点在x轴上的椭圆的一个顶点为A(2,0),其长轴长是短轴长的2倍,求椭圆的标准方程.
(2)已知双曲线的一条渐近线方程是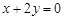 ,并经过点
,并经过点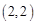 ,求此双曲线的标准方程.
,求此双曲线的标准方程.
函数 的最小正周期为
的最小正周期为 ,其图像经过点
,其图像经过点
(1)求 的解析式;
的解析式;
(2)若 且
且 为锐角,求
为锐角,求 的值.
的值.
已知函数
(Ⅰ)若 在
在 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围;
(Ⅱ)当 时,方程
时,方程 有实根,求实数
有实根,求实数 的最大值.
的最大值.
已知函数 .
.
(1)若函数 在
在 处取得极值,且函数
处取得极值,且函数 只有一个零点,求
只有一个零点,求 的取值范围.
的取值范围.
(2)若函数 在区间
在区间 上不是单调函数,求
上不是单调函数,求 的取值范围.
的取值范围.
统计表明:某种型号的汽车在匀速行驶中每小时的耗油量 (升)关于行驶速度
(升)关于行驶速度 (千米/每小时)的函数解析式可以表示为
(千米/每小时)的函数解析式可以表示为 ,已知甲、乙两地相距100千米.
,已知甲、乙两地相距100千米.
(1)当汽车以40千米/小时的速度行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大速度行驶时,从甲地到乙地耗油最少?最少为多少升?
已知 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,若
,若 ,
, 有
有 恒成立.
恒成立.
(1)判断 在
在 上是增函数还是减函数,并证明你的结论;
上是增函数还是减函数,并证明你的结论;
(2)若 对所有
对所有 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。