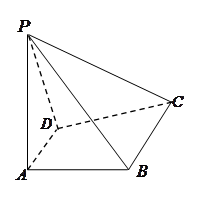
如图,已知四棱锥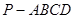 中,
中,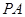 ⊥平面
⊥平面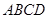 ,
, 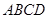 是直角梯形,
是直角梯形, ,
,
 90º,
90º,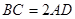 .
.
(1)求证: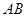 ⊥
⊥ ;
;
(2)在线段 上是否存在一点
上是否存在一点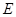 ,使
,使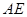 //平面
//平面 ,
,
若存在,指出点 的位置并加以证明;若不存在,请说明理由.
的位置并加以证明;若不存在,请说明理由.
若 ,求函数f(x)=
,求函数f(x)=  的值域.
的值域.
(本小题满分13分)
已知函数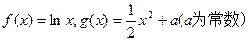 ,若直线
,若直线 与
与 的图象都相切,且
的图象都相切,且 与
与 的图象相切于定点
的图象相切于定点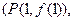
(1)求直线 的方程及a的值;
的方程及a的值;
(2)当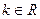 时,讨论关于x的方程
时,讨论关于x的方程 的实数解的个数.
的实数解的个数.
(本小题满分13分)
某化工企业生产某种产品,生产每件产品的成本为3元,根据市场调查,预计每件产品的出厂价为x元(7≤x≤10)时,一年的产量为(11 – x)2万件;若该企业所生产的产品能全部销售,则称该企业正常生产;但为了保护环境,用于污染治理的费用与产量成正比,比例系数为常数a (1≤a≤3).
(Ⅰ)求该企业正常生产一年的利润L (x)与出厂价x的函数关系式;

(Ⅱ)当每件产品的出厂价定为多少元时,企业一年的利润最大,并求最大利润.
已知y = f (x)是定义在[–1,1]上的奇函数,x∈[0,1]时,f (x) =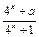 .
.
(1)求x∈[–1,0)时,y = f (x)解析式,并求y = f (x)在[0,1]上的最大值.
(2)解不等式f (x)>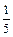 .
.
已知函数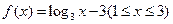 ,设
,设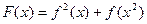

.(1)求F(x)的最大值及最小值.
(2) 已知条件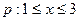 ,条件
,条件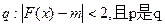 的充分条件,求实数m的取值范围.
的充分条件,求实数m的取值范围. 

