已知定义在实数集上的函数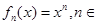 N
N ,其导函数记为
,其导函数记为 ,且满足
,且满足
 ,其中
,其中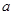 、
、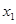 、
、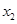 为常数,
为常数,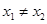 .设函数
.设函数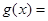
 R且
R且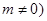 .
.
(Ⅰ)求实数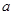 的值;
的值;
(Ⅱ)若函数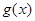 无极值点,其导函数
无极值点,其导函数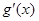 有零点,求m的值;
有零点,求m的值;
(Ⅲ)求函数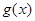 在
在 的图象上任一点处的切线斜率k的最大值
的图象上任一点处的切线斜率k的最大值
(本小题满分12分)
若实数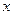 、
、 、
、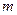 满足
满足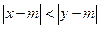 ,则称
,则称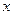 比
比 接近
接近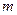 。例如:
。例如: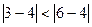 ,则3比6接近4。请证明:对任意两个不相等的正数
,则3比6接近4。请证明:对任意两个不相等的正数 、
、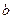 ,
, 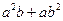 比
比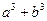 接近
接近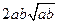 ;
;
(本小题满分12分)
某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为 .甲、乙、丙三位同学每人购买了一瓶该饮料。
.甲、乙、丙三位同学每人购买了一瓶该饮料。
(Ⅰ)求甲中奖且乙、丙都没有中奖的概率;
(Ⅱ)求中奖人数ξ的分布列及数学期望Eξ.
(本小题满分10分)
已知函数 。
。
(1)若函数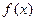 得值不大于1,求
得值不大于1,求 得取值范围;
得取值范围;
(2)若不等式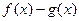
 的解集为R,求
的解集为R,求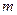 的取值范围。
的取值范围。
设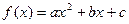 ,当
,当 时,总有
时,总有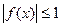 ,求证:
,求证: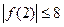 。
。
已知极坐标系的极点O与直角坐标系的原点重合,极轴与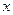 轴的正半轴重合,曲线
轴的正半轴重合,曲线 与曲线
与曲线 (参数
(参数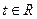 )交于A、B两点,
)交于A、B两点,
(1)求证: ;
;
(2)求 的外接圆的标准方程。
的外接圆的标准方程。