如图,椭圆 的焦点在x轴上,左右顶点分别为A1,A,上顶点B,抛物线C1,C2分别以A1,B为焦点,其顶点均为坐标原点O,C1与C2相交于直线
的焦点在x轴上,左右顶点分别为A1,A,上顶点B,抛物线C1,C2分别以A1,B为焦点,其顶点均为坐标原点O,C1与C2相交于直线 上一点P.
上一点P.
(1)求椭圆C及抛物线C1,C2的方程;
(2)若动直线l与直线OP垂直,且与椭圆C交于不同两点M,N,已知点 ,求
,求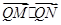 的最小值.
的最小值.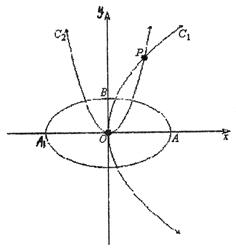
已知函数f(x)=(2cos2x-1)sin2x+ cos4x.
cos4x.
(1)求f(x)的最小正周期及最大值;
(2)若α∈( ,π),且f(α)=
,π),且f(α)= ,求α的值.
,求α的值.
设函数f(θ)= sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
(1)若点P的坐标为( ,
, ),求f(θ)的值;
),求f(θ)的值;
(2)若点P(x,y)为平面区域Ω: 上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
设函数f(x)=Asin(ωx+ )(其中A>0,ω>0,-π<
)(其中A>0,ω>0,-π< ≤π)在x=
≤π)在x= 处取得最大值2,其图象与x轴的相邻两个交点的距离为
处取得最大值2,其图象与x轴的相邻两个交点的距离为 .
.
(1)求f(x)的解析式;
(2)求函数g(x)= 的值域.
的值域.
设函数f(x)=sin2ωx+2 sinωx·cosωx-cos2ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
sinωx·cosωx-cos2ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈( ,1).
,1).
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点( ,0),求函数f(x)的值域.
,0),求函数f(x)的值域.
已知向量a=(cosx,- ),b=(
),b=( sinx,cos2x),x∈R,设函数f(x)=a·b.
sinx,cos2x),x∈R,设函数f(x)=a·b.
(1)求f(x)的最小正周期.
(2)求f(x)在[0, ]上的最大值和最小值.
]上的最大值和最小值.