设函数f(x)=sin2ωx+2 sinωx·cosωx-cos2ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
sinωx·cosωx-cos2ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈( ,1).
,1).
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点( ,0),求函数f(x)的值域.
,0),求函数f(x)的值域.
在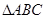 中,角
中,角 所对的边分别为
所对的边分别为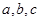 且满足
且满足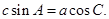
(1)求角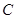 的大小;
的大小;
(2)求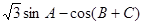 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角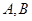 的大小.
的大小.
在△ABC中,角 的对应边分别是
的对应边分别是 满
满 .
.
(1)求角 的大小;
的大小;
(2)已知等差数列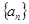 的公差不为零,若
的公差不为零,若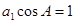 ,且
,且 成等比数列,求
成等比数列,求 的前
的前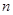 项和
项和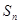 .
.
(本小题满分12分)已知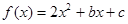 ,不等式
,不等式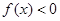 的解集是
的解集是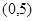 ,
,
(1)求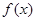 的解析式;
的解析式;
(2)若对于任意 ,不等式
,不等式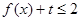 恒成立,求
恒成立,求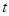 的取值范围.
的取值范围.
已知函数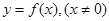 对于任意的
对于任意的 且
且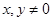 满足
满足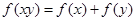 .
.
(Ⅰ)求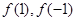 的值;
的值;
(Ⅱ)判断函数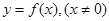 的奇偶性;
的奇偶性;
(Ⅲ)若函数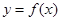 在
在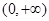 上是增函数,解不等式
上是增函数,解不等式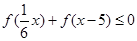 .
.
已知函数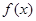 是定义在R上的偶函数,且当
是定义在R上的偶函数,且当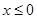 时,
时,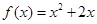 .
.
(Ⅰ)现已画出函数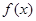 在y轴左侧的图象,如图所示,请补出完整函数
在y轴左侧的图象,如图所示,请补出完整函数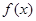 的图象,并根据图象写出函数
的图象,并根据图象写出函数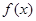 的增区间;
的增区间;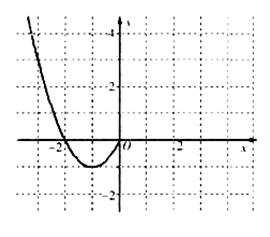
(Ⅱ)求出函数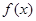 的解析式和值域.
的解析式和值域.