(本题满分l2分)某校学生到距离学校12km的科技馆,出租车的收费标准如下:出租车的行程在3km以内(包括3km),收费为4.5元;3km以上每增加1km(不足1km以1km计算)另收费0.5元.
(1)写出出租车行驶的里程数 (
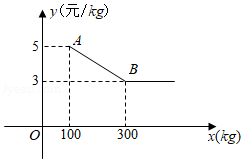
( ≥3km)与费用
≥3km)与费用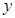 (元)之间的函数关系式.
(元)之间的函数关系式.
(2)身上仅有10元钱,乘出租车到科技馆的车费够不够?
(3)如果出租车行驶了7.4km,问该收多少钱?
已知一次函数 和反比例函数 .
(1)如图1,若 ,且函数 、 的图象都经过点 .
①求 , 的值;
②直接写出当 时 的范围;
(2)如图2,过点 作 轴的平行线 与函数 的图象相交于点 ,与反比例函数 的图象相交于点 .
①若 ,直线 与函数 的图象相交点 .当点 、 、 中的一点到另外两点的距离相等时,求 的值;
②过点 作 轴的平行线与函数 的图象相交于点 .当 的值取不大于1的任意实数时,点 、 间的距离与点 、 间的距离之和 始终是一个定值.求此时 的值及定值 .

小李经营一家水果店,某日到水果批发市场批发一种水果.经了解,一次性批发这种水果不得少于 ,超过 时,所有这种水果的批发单价均为3元 .图中折线表示批发单价 (元 与质量 的函数关系.
(1)求图中线段 所在直线的函数表达式;
(2)小李用800元一次可以批发这种水果的质量是多少?
如图,在平面直角坐标系 中,二次函数图象的顶点坐标为 ,该图象与 轴相交于点 、 ,与 轴相交于点 ,其中点 的横坐标为1.
(1)求该二次函数的表达式;
(2)求 .

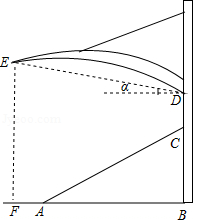
某体育看台侧面的示意图如图所示,观众区 的坡度 为 ,顶端 离水平地面 的高度为 ,从顶棚的 处看 处的仰角 ,竖直的立杆上 、 两点间的距离为 , 处到观众区底端 处的水平距离 为 .求:
(1)观众区的水平宽度 ;
(2)顶棚的 处离地面的高度 . , ,结果精确到
小明代表学校参加“我和我的祖国”主题宣传教育活动.该活动分为两个阶段,第一阶段有“歌曲演唱”、“书法展示”、“器乐独奏”3个项目(依次用 、 、 表示),第二阶段有“故事演讲”、“诗歌朗诵”2个项目(依次用 、 表示),参加人员在每个阶段各随机抽取一个项目完成.用画树状图或列表的方法列出小明参加项目的所有等可能的结果,并求小明恰好抽中 、 两个项目的概率.