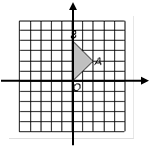
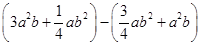如图,正方形网格中的每个小正方形的边长都是1,在 平面直角坐标系中,已知,ΔABO的三个顶点的坐标分别为A(2,2),B(0,4),O(0,0);
平面直角坐标系中,已知,ΔABO的三个顶点的坐标分别为A(2,2),B(0,4),O(0,0); 画出ΔABO绕点O逆时针旋转900后得到的Δ
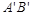 0并写出点A
0并写出点A ,B
,B 的坐标;
的坐标;求旋转过程中动点B所经过的路径长。
计算:
(1)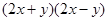 (2)
(2)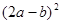
(3) (4)4-
(4)4- -(2-
-(2- )+
)+
阅读理解填空:
(1)如图,已知AB∥CD,∠1=∠2,试说明EP∥FQ.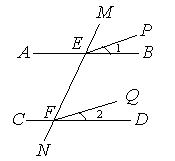
证明:∵AB∥CD,
∴∠MEB=∠MFD( )
又∵∠1=∠2,
∴∠MEB-∠1=∠MFD-∠2,
即∠MEP=∠______
∴EP∥_____.( )
(2)如图,EF∥AD,∠1=∠2,∠BAC=70 o,求∠AGD.
解:∵EF∥AD,
∴∠2=()
又∵∠1=∠2,
∴∠1=∠3,
∴AB∥()
∴∠BAC+=180 o()
∵∠BAC=70 o,
∴∠AGD=。
如图, 与
与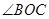 是邻补角,OD、OE分别是
是邻补角,OD、OE分别是 与
与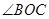 的平分线,试判断OD与OE的位置关系,并说明理由.
的平分线,试判断OD与OE的位置关系,并说明理由.
先化简,再求值: ,其中a=-2。
,其中a=-2。
计算:
(1)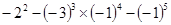
(2)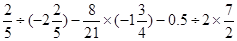
(3)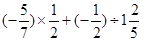
(4)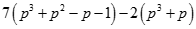
(5)
(6)