某校为了探索一种新的教学模式，进行了一项课题实验，甲班为实验班，乙班为对比班，甲乙两班的人数均为50人，一年后对两班进行测试，测试成绩的分组区间为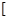
80,90
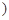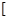、90,100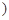、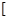100,110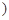、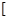110,12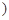0、120,130，由此得到两个班测试成绩的频率分布直方图：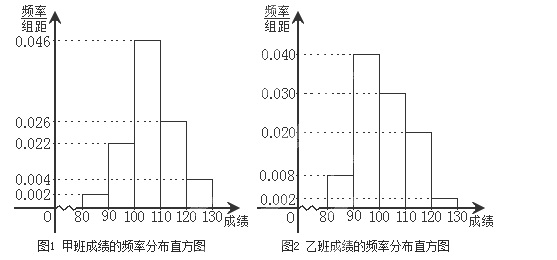
（1）完成下面2×2列联表，你能有97.5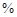
的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗？并说明理由；
| |
成绩小于100分 |
成绩不小于100分 |
合计 |
| 甲班 |
 |
 |
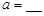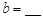50 |
| 乙班 |
 |
 |
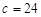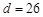50 |
| 合计 |
 |
 |
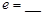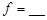100 |
（2）根据所给数据可估计在这次测试中，甲班的平均分是105.8，请你估计乙班的平均分，并计算两班平均分相差几分？
附：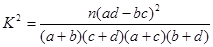
，其中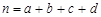
 |
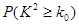0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
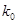2.072 |
2.706 |
3.841 |
5.204 |
6.635 |
7.879 |
10.828 |
设
满足约束条件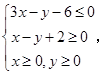
若目标函数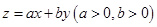
的最大值为10，则
的最小值为
抛物线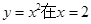
处的切线与抛物线以及
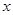轴所围成的曲边图形的面积为
（本小题满分12分）已知
，函数
，
．
（1）若曲线
与曲线
在它们的交点
处的切线重合，求
，
的值；
（2）设
，若对任意的
，且
，都有
，求的取值范围．
（本小题满分12分）已知椭圆C:
过点
，离心率为
，点
分别为其左右焦点.
（1）求椭圆C的标准方程;
（2）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆C恒有两个交点
,且
？若存在，求出该圆的方程；若不存在，请说明理由.
（本小题满分12分）从某小区抽取100个家庭进行月用电量调查，发现其月用电量都在50度至350度之间，频率分布直方图如图所示．
（1）根据直方图求
的值，并估计该小区100个家庭的月均用电量（同一组中的数据用该组区间的中点值作代表）；
（2）从该小区已抽取的100个家庭中, 随机抽取月用电量超过300度的2个家庭，参加电视台举办的环保互动活动，求家庭甲（月用电量超过300度）被选中的概率．