已知椭圆
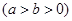 的离心率为
的离心率为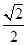 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线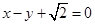 相切.
相切.
(1)求椭圆 的方程;
的方程;
(2)若过点 (2,0)的直线与椭圆
(2,0)的直线与椭圆 相交于两点
相交于两点 ,设
,设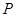 为椭圆上一点,且满足
为椭圆上一点,且满足 (O为坐标原点),当
(O为坐标原点),当 <
<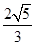 时,求实数
时,求实数 取值范围.
取值范围.
(本小题满分10分)已知函数 ,且当
,且当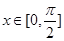 时,
时,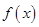 的最小值为2,
的最小值为2,
(1)求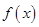 的单调递增区间;
的单调递增区间;
(2)先将函数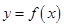 的图象上的点纵坐标不变,横坐标缩小到原来的
的图象上的点纵坐标不变,横坐标缩小到原来的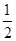 ,再把所得的图象向右平移
,再把所得的图象向右平移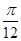 个单位,得到函数
个单位,得到函数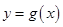 的图象,求方程
的图象,求方程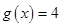 在区间
在区间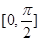 上所有根之和.
上所有根之和.
(本小题满分12分).已知函数 (
(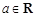 ).
).
(1)若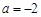 ,求曲线
,求曲线 在点
在点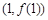 处的切线方程;
处的切线方程;
(2)若不等式 对任意
对任意 恒成立.
恒成立.
(ⅰ)求实数 的取值范围;
的取值范围;
(ⅱ)试比较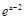 与
与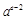 的大小,并给出证明(
的大小,并给出证明(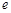 为自然对数的底数,
为自然对数的底数, ).
).
(本小题满分12分)设△ABC三个内角A、B、C所对的边分别为a,b,c.已知C=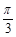 ,acosA=bcosB.
,acosA=bcosB.
(1)求角B的大小;
(2)如图,在△ABC内取一点P,使得PB=2.过点P分别作直线BA、BC的垂线PM、PN,垂足分别是M、N.设∠PBA=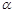 ,求PM+PN的最大值及此时
,求PM+PN的最大值及此时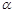 的取值.
的取值.
(本小题满分12分)设数列{an}的前n项和为Sn=n2,{bn}为等比数列,且a1=b1,b2(a2-a1)=b1.
(1)求数列{an},{bn}的通项公式.
(2)设cn=an·bn,求数列{cn}的前n项和Tn.
(本小题满分12分)已知函数f(x)=log3 .
.
(1)求函数f(x)的定义域.
(2)判断函数f(x)的奇偶性.
(3)当x∈ 时,函数g(x)=f(x),求函数g(x)的值域.
时,函数g(x)=f(x),求函数g(x)的值域.