在△ABC中,∠A= ∠C=
∠C= ∠ABC,BD是∠ABC的平分线,求∠A及∠BDC的度数.
∠ABC,BD是∠ABC的平分线,求∠A及∠BDC的度数.
如图,△ABC中,BD是∠ABC的角平分线,DE∥BC交AB于E,∠A=60°,∠BDC=95°,求△BDE各内角的度数.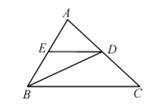
如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.若∠B=35°,∠E=20°,求∠BAC的度数.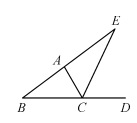
(本题9分)如图,正方形ABCD(四条边相等,四个角是直角)的边长为7cm,点M在边DC上,且CM=2cm,过点M作 ME⊥DC,交BD于点E.,动点P从点D出发沿DC边向M点运动,速度为每秒2 cm,当动点P到达M点时,运动停止.连接EP,EC.在此过程中,设P点运动时间为t秒.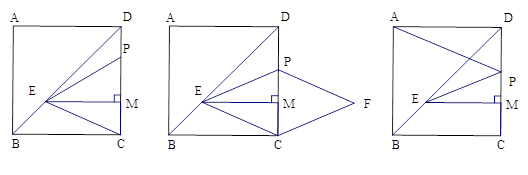
(1)EM = cm,
PC = cm(用含t的代数式表示),
当t = 秒时,△EPC的面积为15?
(2)将△EPC沿CP翻折后,点E的对应点为F点,若PF∥EC,则△EPC为 三角形,请说明理由并求此时t为何值.
(3)是否存在某一时刻,使得P点到A点、E点的距离之和最短?如果存在,直接写出PA+PE的最小值,如果不存在,请说明理由.
(本题8分)在一次数学课上,老师在屏幕上出示了一个例题:在△ABC中,D,E分别是AB,AC上的一点,BE与CD交于点O,画出图形(如图),给出下列四个条件:①∠DBO=∠ECO;②∠BDO=∠CEO;③BD=CE;④OB=OC.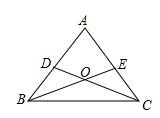
(1)要求同学从这四个等式中选出两个作为已知条件,可判定△ABC是等腰三角形.
请你用序号在横线上写出所有情形.答:
(2)选择第(1)题中的一种情形,说明△ABC是等腰三角形的理由,并写出解题过程.
解:我选择 .
证明: