小华观察钟面(图1),了解到钟面上的分针每小时旋转360度,时针毎小时旋转30度.他为了进一步探究钟面上分针与时针的旋转规律,从下午2:00开始对钟面进行了一个小时的观察.为了探究方便,他将分针与分针起始位置OP(图2)的夹角记为y1,时针与OP的夹角记为y2度(夹角是指不大于平角的角),旋转时间记为t分钟.观察结束后,他利用获得的数据绘制成图象(图3),并求出y1与t的函数关系式: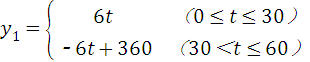
请你完成:求出图3中y2与t的函数关系式;
直接写出A、B两点的坐标,并解释这两点的实际意义;
若小华继续观察一个小时,请你在题图3中补全图象.
在△ABC中,AB=AC,∠A=300,将线段BC绕点B逆时针旋转600得到线段BD,再将线段BD平移到EF,使点E在AB上,点F在AC上.
(1)如图1,直接写出∠ABD和∠CFE的度数;
(2)在图1中证明:AE=CF;
(3)如图2,连接CE,判断△CEF的形状并加以证明.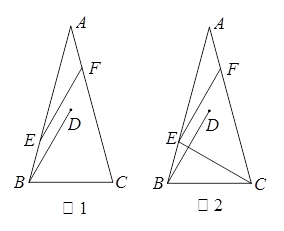
已知关于 的一元二次方程
的一元二次方程 .
.
(1)求证:方程总有两个实数根;
(2)若m为整数,当此方程有两个互不相等的负整数根时,求m的值;
(3)在(2)的条件下,设抛物线 与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.点O为坐标原点,点P在直线BC上,且OP=
与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.点O为坐标原点,点P在直线BC上,且OP= BC,求点P的坐标.
BC,求点P的坐标.
问题:如图1,在△ABC中,BE平分∠ABC,CE平分∠ACB.若∠A=800,则∠BEC=;若∠A=n0,则∠BEC=.
探究:
(1)如图2,在△ABC中,BD、BE三等分∠ABC,CD、CE三等分∠ACB.若∠A=n0,则∠BEC=;
(2)如图3,在△ABC中,BE平分∠ABC,CE平分外角∠ACM.若∠A=n0,则∠BEC=;
(3)如图4,在△ABC中,BE平分外角∠CBM,CE平分外角∠BCN.若∠A=n0,则∠BEC=.
如图,⊙O是△ABC的外接圆,AB=AC,过点A作AD∥BC交BO的延长线于点D.
(1)求证:AD是⊙O的切线;
(2)若⊙O的半径OB=5,BC=8,求线段AD的长.
保障房建设是民心工程,某市从2009年加快保障房建设工程.现统计了该市从2009年到2013年这5年新建保障房情况,绘制成如图1、2所示的折线统计图和不完整的条形统计图.
(1)小颖看了统计图后说:“该市2012年新建保障房的套数比2011年少了.”你认为小颖的说法正确吗?请说明理由;
(2)求2012年新建保障房的套数,并补全条形统计图;
(3)求这5年平均每年新建保障房的套数.