已知抛物线 的焦点为F,其准线与x轴交于点M,过点M作斜率为k的直线l交抛物线于A、B两点,.
的焦点为F,其准线与x轴交于点M,过点M作斜率为k的直线l交抛物线于A、B两点,.
(Ⅰ)求k的取值范围
(Ⅱ)若弦AB的中点为P,AB的垂直平分线与x轴交于点E( O),求证:
O),求证:
(本小题满分16分)如图,已知矩形ABCD中,AB=10,BC=6,沿矩形的对角线BD把 折起,使A移到A1点,且A1在平面BCD上的射影O恰好在CD上。
折起,使A移到A1点,且A1在平面BCD上的射影O恰好在CD上。
(Ⅰ)求证: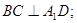
(Ⅱ)求证:平面 平面
平面
(本小题满分14分)已知:在函数 的图象上,以
的图象上,以 为切点的切线的倾斜角为
为切点的切线的倾斜角为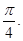
(Ⅰ)求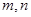 的值;
的值;
(Ⅱ)是否存在最小的正整数 ,使得不等式
,使得不等式 恒成立?如果存在,请求出最小的正整数
恒成立?如果存在,请求出最小的正整数 ,如果不存在,请说明理由。
,如果不存在,请说明理由。
(本小题满分14分)在直角坐标系中,O为坐标原点,设直线 经过点
经过点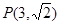 ,且与
,且与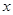 轴交于点F(2,0)。
轴交于点F(2,0)。
(Ⅰ)求直线 的方程;
的方程;
(Ⅱ)如果一个椭圆经过点P,且以点F为它的一个焦点,求椭圆的标准方程。
(本小题满发14分)已知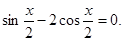
(Ⅰ)求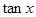 的值;
的值;
(Ⅱ)求 的值
的值
求函数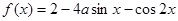 的最大值和最小值。
的最大值和最小值。