列方程或方程组解应用题:
中国2010年上海世博会第三期预售平日门票分为普通票和优惠票,其中普通票每张150元人民币,优惠票每张90元人民币.某日一售票点共售出1000张门票,总收入12.6万元人民币.那么,这一售票点当天售出的普通票和优惠票各多少张?
注:优惠票的适用对象包括残疾人士、老年人(1950年12月31日前出生的)、学生、身高超过1.20米的儿童、现役军人.
若a, b之间有9个整数(不含a, b本身),则a—b的范围是____
(1)填空:1—2+3—4+……+49—50=_____________;
1—2+3—4+……+99—100+101=_____________;
(2)计算: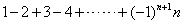
如图所示,用三种大小不同的六个正方形和一个缺角的正方形拼成长方形ABCD,其中,GH="2cm," GK="2cm," 设BF="x" cm,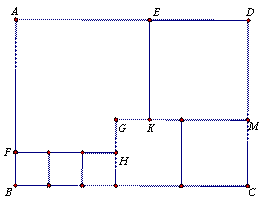
(1)用含x的代数式表示CM=_____________cm,DM=_____________cm.
(2)若DC=10cm,求x的值.
(3)求长方形ABCD的面积.
已知: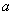 ,
,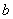 互为相反数,
互为相反数,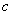 ,
,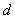 互为倒数,
互为倒数,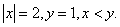
求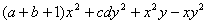 的值.
的值.
列方程解应用题
种一批树苗,如果每人种15棵,则剩下6棵没人种,如果每人种17棵,则缺6棵树苗,问有多少人种树?