如左图：直线ykx4k（k≠0）交x轴于点A，交y轴于点C，-优题课

如左图：直线y=kx+4k（k≠0）交x轴于点A，交y轴于点C，点M（2，m）为直线AC上一点，过点M的直线BD交x轴于点B，交y轴于点D．
（1）求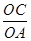的值（用含有k的式子表示．）；
（2）若S_△BOM=3S_△DOM，且k为方程（k+7）（k+5）﹣（k+6）（k+5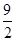）=的根，求直线BD的解析式．
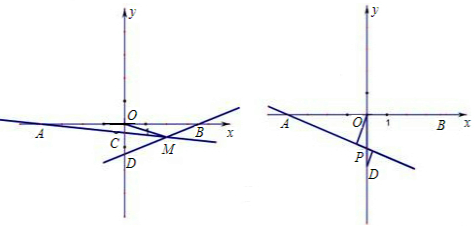
（3）如右图，在（2）的条件下，P为线段OD之间的动点（点P不与点O和点D重合），OE上AP于E，DF上AP于F，下列两个结论：①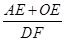值不变；②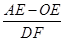值不变，请你判断其中哪一个结论是正确的，并说明理由并求出其值．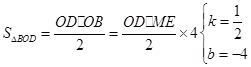
．

科目数学题型解答题难度中等

（1）计算： ${(\frac{1}{2})}^{- 2} + {(3.14 - π)}^{0} + | 3 - \sqrt{12} | - 4 \sin 60 °$ ．

（2）先化简，再求值： $(\frac{1}{x - 1} - x + 1) \div \frac{x - 2}{x^{2} - 1}$ ，其中 $x = \sqrt{2} - 1$ ．

如图，已知二次函数的图象与 $x$ 轴交于 $A$ 和 $B (- 3, 0)$ 两点，与 $y$ 轴交于 $C (0, - 3)$ ，对称轴为直线 $x = - 1$ ，直线 $y = - 2 x + m$ 经过点 $A$ ，且与 $y$ 轴交于点 $D$ ，与抛物线交于点 $E$ ，与对称轴交于点 $F$ ．

（1）求抛物线的解析式和 $m$ 的值；

（2）在 $y$ 轴上是否存在点 $P$ ，使得以 $D$ 、 $E$ 、 $P$ 为顶点的三角形与 $ΔAOD$ 相似，若存在，求出点 $P$ 的坐标；若不存在，试说明理由；

（3）直线 $y = 1$ 上有 $M$ 、 $N$ 两点 $(M$ 在 $N$ 的左侧），且 $MN = 2$ ，若将线段 $MN$ 在直线 $y = 1$ 上平移，当它移动到某一位置时，四边形 $MEFN$ 的周长会达到最小，请求出周长的最小值（结果保留根号）．

如图， $⊙ O$ 的半径为1，点 $A$ 是 $⊙ O$ 的直径 $BD$ 延长线上的一点， $C$ 为 $⊙ O$ 上的一点， $AD = CD$ ， $∠ A = 30 °$ ．

（1）求证：直线 $AC$ 是 $⊙ O$ 的切线；

（2）求 $ΔABC$ 的面积；

（3）点 $E$ 在 $\hat{BND}$ 上运动（不与 $B$ 、 $D$ 重合），过点 $C$ 作 $CE$ 的垂线，与 $EB$ 的延长线交于点 $F$ ．

①当点 $E$ 运动到与点 $C$ 关于直径 $BD$ 对称时，求 $CF$ 的长；

②当点 $E$ 运动到什么位置时， $CF$ 取到最大值，并求出此时 $CF$ 的长．

如图，一次函数 $y_{1} = kx + b (k \neq 0)$ 与反比例函数 $y_{2} = \frac{m}{x} (m \neq 0)$ 的图象交于

点 $A (1, 2)$ 和 $B (- 2, a)$ ，与 $y$ 轴交于点 $M$ ．

（1）求一次函数和反比例函数的解析式；

（2）在 $y$ 轴上取一点 $N$ ，当 $ΔAMN$ 的面积为3时，求点 $N$ 的坐标；

（3）将直线 $y_{1}$ 向下平移2个单位后得到直线 $y_{3}$ ，当函数值 $y_{1} > y_{2} > y_{3}$ 时，求 $x$ 的取值范围．

小明周末与父母一起到遂宁湿地公园进行数学实践活动，在 $A$ 处看到 $B$ 、 $C$ 处各有一棵被湖水隔开的银杏树，他在 $A$ 处测得 $B$ 在北偏西 $45 °$ 方向， $C$ 在北偏东 $30 °$ 方向，他从 $A$ 处走了20米到达 $B$ 处，又在 $B$ 处测得 $C$ 在北偏东 $60 °$ 方向．

（1）求 $∠ C$ 的度数；

（2）求两颗银杏树 $B$ 、 $C$ 之间的距离（结果保留根号）．