.(本小题满分12分)
某种产品的广告费支出 与销售额
与销售额 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
 |
2 |
4 |
5 |
6 |
8 |
 |
30 |
40 |
60 |
50 |
70 |
(Ⅰ)求回归直线方程;
(Ⅱ)试预测广告费支出为10万元时,销售额多大?
(Ⅲ)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对
值不超过5的概率。(参考数据:

 )
)
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上40件产品作为样本,称出它们的重量(单位:克),重量的分组区间为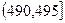 ,
,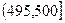 ,…,
,…,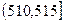 ,由此得到样本的频率分布直方图,如右图所示.
,由此得到样本的频率分布直方图,如右图所示.
(1)根据频率分布直方图,求重量超过505克的产品数量.
(2)在上述抽取的40件产品中任取2件,设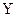 为重量超过505克的产品数量,求
为重量超过505克的产品数量,求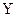 的分布列.
的分布列.
(3)从流水线上任取5件产品,求恰有2件产品的重量超过505克的概率
已知向量 ,
,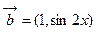 ,函数
,函数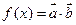 ,
,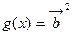 .
.
(Ⅰ)求函数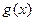 的最小正周期;
的最小正周期;
(Ⅱ)在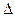
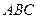 中,
中, 分别是角
分别是角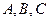 的对边,且
的对边,且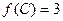 ,
, ,
,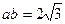 ,且
,且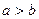 ,求
,求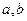 的值.
的值.
(本小题满分14分)已知函数 .
.
(Ⅰ)当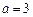 时,求
时,求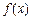 的单调递增区间;
的单调递增区间;
(Ⅱ)求证:曲线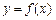 总有斜率为
总有斜率为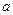 的切线;
的切线;
(Ⅲ)若存在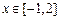 ,使
,使 成立,求
成立,求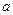 的取值范围.
的取值范围.
如图,已知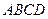 为平行四边形,
为平行四边形,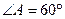 ,
,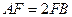 ,
,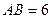 ,点
,点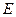 在
在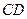 上,
上, ,
, ,
,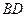 交
交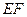 于点
于点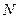 ,现将四边形
,现将四边形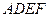 沿
沿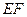 折起,使点
折起,使点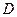 在平面
在平面 上的射影恰在直线
上的射影恰在直线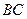 上.
上.
(Ⅰ) 求证: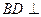 平面
平面 ;
;
(Ⅱ) 求折后直线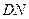 与直线
与直线 所成角的余弦值;
所成角的余弦值;
(Ⅲ) 求三棱锥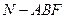 的体积.
的体积.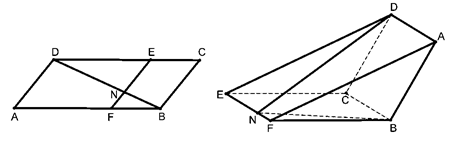
(本小题满分12分)
已知向量
(1)求a·b及|a+b|;
(2)若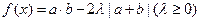 的最小值是
的最小值是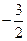 ,求实数
,求实数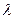 的值。
的值。