已知△ABC和△ADE是等腰直角三角形，∠ACB=∠ADE=90°，点F为BE中点，连结DF、CF. （1）如图1, 当点D在AB上，点E在AC上，请直接写出此时线段DF、CF的数量关系和位置关系（不用证明）；
（2）如图2，在（1）的条件下将△ADE绕点A顺时针旋转45°时，请你判断此时（1）中的结论是否仍然成立，并证明你的判断；
（3）如图3，在（1）的条件下将△ADE绕点A顺时针旋转90°时，若AD=1，AC=
，求此时线段CF的长(直接写出结果).
解不等式组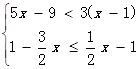
，并将解集在数轴上表示出来．
解不等式组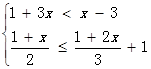
，并写出它的所有整数解．
解不等式组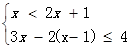
，并把解集在数轴上表示出来．
有红、白两种颜色的小球若干个，已知白球的个数比红球少，但白球的个数的2倍比红球多；若给每个白球都写上数字“2”，给每个红球都写上数字“3”（每个小球只能写上一个数字），结果所有小球写的数字总和为60，那么白球和红球各是多少个？
两个男孩各骑一辆自行车，从相距20英里的两个地方，开始沿直线相向骑行．在他们起步的那一瞬间，一辆自行车车把上的一只苍蝇，开始向另一辆自行车径直飞去．它一到达另一辆自行车车把，就立即转向往回飞行．这只苍蝇如此往返，在两辆自行车的车把之间来回飞行，直到两辆自行车相遇为止．如果每辆自行车都以每小时10英里等速前进，苍蝇以每小时15英里等速飞行，那么，苍蝇总共飞行了多少英里？