在 中,已知内角
中,已知内角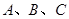 所对的边分别为
所对的边分别为 ,向量
,向量 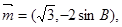
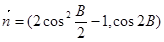 ,且
,且 //
//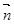 ,
,  为锐角.
为锐角.
(1)求角 的大小; (2)设
的大小; (2)设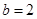 ,求
,求 的面积
的面积 的最大值.
的最大值.
在 中,角A,B,C所对的边分别为a,b,c, 已知a,b,c成等比数列,且
中,角A,B,C所对的边分别为a,b,c, 已知a,b,c成等比数列,且 .
.
(Ⅰ)求角B的大小;
(Ⅱ)若
 ,求
,求 的面积最大值.
的面积最大值.
抛物线 :
: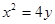 ,直线
,直线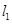 :
: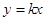 交
交 于点
于点 ,交准线于点
,交准线于点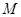 .过点
.过点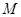 的直线
的直线 与抛物线
与抛物线 有唯一的公共点
有唯一的公共点 (
( ,
, 在对称轴的两侧),且与
在对称轴的两侧),且与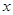 轴交于点
轴交于点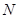 .
.
(Ⅰ)求抛物线 的准线方程;
的准线方程;
(Ⅱ)求 的取值范围.
的取值范围.
已知 ,函数
,函数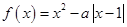 .
.
(Ⅰ)当 时,求函数
时,求函数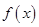 的最小值;
的最小值;
(Ⅱ)当 时,讨论
时,讨论 的图象与
的图象与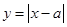 的图象的公共点个数.
的图象的公共点个数.
如图,在三棱锥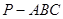 中,△
中,△ 是边长为
是边长为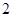 的正三角形,
的正三角形,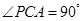 ,
,  ,
, 分别为
分别为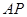 ,
,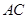 的中点,
的中点, ,
,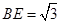 .
. 
(Ⅰ)求证: 平面
平面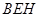 ;
;
(Ⅱ)求直线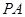 与平面
与平面 所成角的正弦值.
所成角的正弦值.
已知数列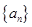 满足:
满足: ,
,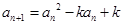 ,(
,( ),
), ,
,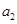 ,
, 分别是公差不为零的等差数列
分别是公差不为零的等差数列 的前三项.
的前三项.
(Ⅰ)求 的值;
的值;
(Ⅱ)求证:对任意的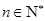 ,
,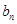 ,
, ,
,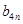 不可能成等比数列.
不可能成等比数列.