已知关于x的函数f(x)=-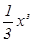 +bx2+cx+bc,其导函数为
+bx2+cx+bc,其导函数为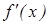 .令g(x)=∣
.令g(x)=∣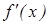 ∣,记函数g(x)在区间[-1、1]上的最大值为M.
∣,记函数g(x)在区间[-1、1]上的最大值为M.
(Ⅰ)如果函数f(x)在x=1处有极值-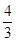 ,试确定b、c的值:
,试确定b、c的值:
(Ⅱ)若∣b∣>1,证明对任意的c,都有M>2:
(Ⅲ)若M≥K对任意的b、c恒成立,试求k的最大值
(附加题)本题满分20分
如图,已知抛物线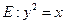
 与圆
与圆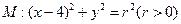 相交于A、B、C、D四个点。
相交于A、B、C、D四个点。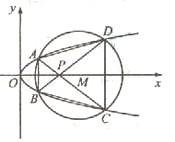
(Ⅰ)求r的取值范围(Ⅱ)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标。
甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束。假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立。已知前2局中,甲、乙各胜1局。
(Ⅰ)求再赛2局结束这次比赛的概率;(Ⅱ)求甲获得这次比赛胜利的概率。

(Ⅰ)求 | z1| 的值以及z1的实部的取值范围;(Ⅱ)若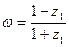 ,求证:
,求证: 为纯虚数
为纯虚数
解不等式
(本小题10分)函数 是偶函数.
是偶函数.
(1)求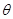 ;
;
(2)将函数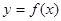 的图像先纵坐标不变,横坐标缩短为原来的
的图像先纵坐标不变,横坐标缩短为原来的 倍,再向左平移
倍,再向左平移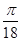 个单位,然后向上平移1个单位得到
个单位,然后向上平移1个单位得到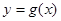 的图像,若关于
的图像,若关于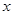 的方程
的方程 有且只有两个不同的根,求
有且只有两个不同的根,求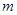 的范围.
的范围.