(附加题)本题满分20分
如图,已知抛物线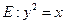
 与圆
与圆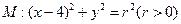 相交于A、B、C、D四个点。
相交于A、B、C、D四个点。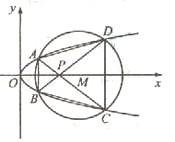
(Ⅰ)求r的取值范围 (Ⅱ)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标。
(本小题满分15分)已知矩形纸片ABCD中,AB=6cm,AD=12cm,将矩形
纸片的右下角折起,使得该角的顶点B落在矩形的边AD上,且折痕MN的
端点M, N分别位于边AB, BC上,设∠MNB=θ,sinθ=t,MN长度为l.
(1)试将l表示为t的函数l=f (t);
(2)求l的最小值.
(本小题满分15分)如图,已知椭圆 :+=1(a>b>0)的长轴AB长为4,离心率e=,O为坐标原点,过B的直线l与x轴垂直.P是椭圆上异于A、B的任意一点,PH⊥x轴,H为垂足,延长HP到点Q使得HP=PQ,连结AQ延长交直线
:+=1(a>b>0)的长轴AB长为4,离心率e=,O为坐标原点,过B的直线l与x轴垂直.P是椭圆上异于A、B的任意一点,PH⊥x轴,H为垂足,延长HP到点Q使得HP=PQ,连结AQ延长交直线 于点M,N为
于点M,N为 的中点.
的中点.
(1)求椭圆 的方程;
的方程;
(2)证明:Q点在以 为直径的圆
为直径的圆 上;
上;
(3)试判断直线QN与圆 的位置关系.
的位置关系.
(本小题满分14分)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,
∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
(1)求证:PC⊥ ;
;
(2)求证:CE∥平面PAB;
(3)求三棱锥P-ACE的体积V.
(本小题满分14分)已知锐角 中的三个内角分别为
中的三个内角分别为 .
.
(1)设·=·,求证: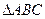 是等腰三角形;
是等腰三角形;
(2)设向量=(2sinC, -), =(cos2C, 2cos2 -1), 且∥, 若sinA=,求sin(-B)的值.
(本小题满分14分)
已知数列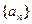 ,
,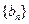 满足
满足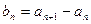 ,其中
,其中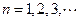 .
.
(Ⅰ)若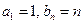 ,求数列
,求数列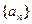 的通项公式;
的通项公式;
(Ⅱ)若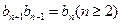 ,且
,且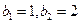 .
.
(ⅰ)记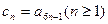 ,求证:数列
,求证:数列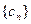 为等差数列;
为等差数列;
(ⅱ)若数列 中任意一项的值均未在该数列中重复出现无数次. 求首项
中任意一项的值均未在该数列中重复出现无数次. 求首项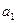 应满足的条件.
应满足的条件.