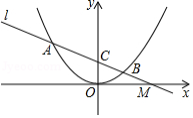
已知一元二次方程x2-4x+3=0的两根是m,n且m<n.如图12,若抛物线y=-x2+bx
+c的图像经过点A(m,0)、B(0,n).求抛物线的解析式.
若(1)中的抛物线与x轴的另一个交点为C.根据图像回答,当x取何值时,抛物线的图像在直线BC的上方?
点P在线段OC上,作PE⊥x轴与抛物线交与点E,若直线BC将△CPE的面积分成相等的两部分,求点P的坐标.

如图,在菱形 中,将对角线 分别向两端延长到点 和 ,使得 .连接 , , , .
求证:四边形 是菱形.

解方程: .
已知 是 斜边 的中点, , ,过点 作 使 , ,连接 并延长 到 ,使 ,连接 , , ,设 与 交于 , 与 交于 .
(1)如图1,当 , , 共线时,求证:
① ;
② ;
(2)如图2,当 , , 不共线时,连接 ,求证: .

如图,已知抛物线 过点 .
(1)求抛物线的解析式;
(2)已知直线 过点 , , 且与抛物线交于另一点 ,与 轴交于点 ,求证: ;
(3)若点 , 分别是抛物线与直线 上的动点,以 为一边且顶点为 , , , 的四边形是平行四边形,求所有符合条件的 点坐标.
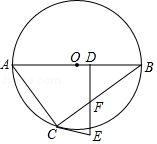
如图,已知 是 的直径, 是 上的一点, 是 上的一点, 于 , 交 于 ,且 .
(1)求证: 是 的切线;
(2)若 , ,圆的半径 ,求切线 的长.