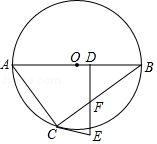
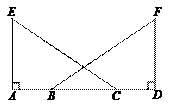如图,已知 是 的直径, 是 上的一点, 是 上的一点, 于 , 交 于 ,且 .
(1)求证: 是 的切线;
(2)若 , ,圆的半径 ,求切线 的长.
如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点D处,点A落在点 处,连结BE.
处,连结BE.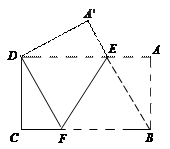
求证:四边形 是菱形;
是菱形;
若AB =" 4" cm,BC =" 8" cm,求折痕EF的长.
如图,△ABC中,AB = AC,AD、AE分别是∠BAC和∠BAC外角的平分线, .
.
(1)求证:DA⊥AE;
(2)试判断AB与DE是否相等?并证明你的结论.
如图,在等边△ABC中,点D、E分别在边BC、AB上,且BD = AE,AD与CE交于点F.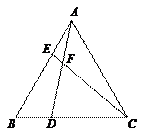
(1)求证:AD = CE;
(2)求∠DFC的度数.
如图所示,在□ABCD中,E、F是对角线AC上两点,且AE = CF.求证:四边形DEBF 是平行四边形.
是平行四边形.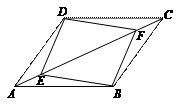
已知:如图,点A、B、C、D在同一条直线上,EA⊥AD,FD⊥AD,AE = DF,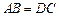 .
.
求证:∠ACE =∠DBF.