已知函数 (
( ,
, ),且函数
),且函数 的最小正周期为
的最小正周期为 .
.
(Ⅰ)求函数 的解析式并求
的解析式并求 的最小值;
的最小值;
(Ⅱ)在 中,角A,B,C所对的边分别为
中,角A,B,C所对的边分别为 ,若
,若 =1,
=1, ,
, 且
且 ,求边长
,求边长 .
.
某校九年级(3)班的师生到距离10千米的山区植树,出发1.5小时后,张锦同学骑自行车从学校按原路追赶队伍,结果他们同时到达植树地点.如果张锦同学骑车的速度比队伍步行的速度的2倍还多2千米.求骑车与步行的速度各是多少?
先化简,再求值: ,其中
,其中 .
.
如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒,当t为何值时,以P、Q、C为顶点的三角形与△ADE相似?
(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
【问题探究】
(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等腰△ABE和等腰△ACD,使AE=AB,AD=AC,∠BAE=∠CAD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.
【深入探究】
(2)如图2,四边形ABCD中,AB=7cm,BC=3cm,∠ABC=∠ACD=∠ADC=45º,求BD的长.
(3)如图3,在(2)的条件下,当△ACD在线段AC的左侧时,求BD的长.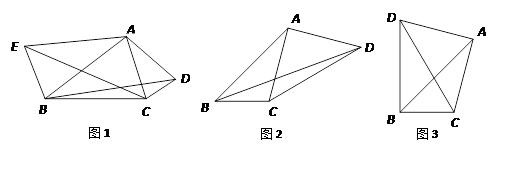
某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.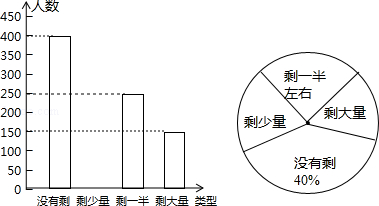
(1)这次被调查的同学共有 名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校18 000名学生一餐浪费的食物可供多少人食用一餐?