某次演唱比赛，需要加试文化科学素质，每位参赛选手需加答3个问题，组委会为每位选手都备有10道不同的题目可供选择，其中有5道文史类题目，3道科技类题目，2道体育类题目，测试时，每位选手从给定的10道题中不放回地随机抽取3次，每次抽取一道题，回答完该题后，再抽取下一道题目作答．
（1）求某选手第二次抽到的不是科技类题目的概率；
（2）求某选手抽到体育类题目数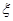
的分布列和数学期望E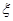
设F（x）=3a
+2bx+c，若a+b+c=0，且F（0）>0，F（1）>0.
求证：a>0，且—2<
<—1.
某射手每次射击击中目标的概率均为
，且每次射击的结果互不影响
（I）假设这名射手射击3次，求至少2次击中目标的概率
（II）假设这名射手射击3次，每次击中目标10分，未击中目标得0分，在3次射击中，若有两次连续击中目标，而另外一次未击中目标，则额外加5分；若3次全部击中，则额外加10分。用随机变量§表示射手射击3次后的总得分，求§的分布列和数学期望。
已知
+
+
+…+
=
（nεN）
（I）求n的值
（II）求二项式 
的一次项
某主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查，统计数据如下表所示
| 积极参加班级工作 |
不太主动参加班级工作 |
|
| 学习积极性高 |
18 |
7 |
| 学习积极性一般 |
6 |
19 |
（I）如果随机抽查这个班的一名学生，那么抽到积极参加班级工作的学生的概率是多少？抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少？
（II）试运用独立性检验的思想方法分析：学生的学习积极性与对待班级工作的态度是否有关？并说明理由
附：
P（ ≥k） |
0.050 |
0.010 |
0.001 |
= |
| k |
3.841 |
6.635 |
10.828 |
已知复数Z=a+bi（a，b εR），且
—（i—1）a+3b+2i=0
（I）求复数Z
（II）若Z+
εR,求实数m的值.