已知函数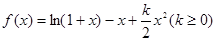 。
。
(1)当 时,求曲线
时,求曲线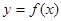 在点
在点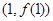 处的切线方程;
处的切线方程;
(2)求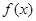 的单调区间。
的单调区间。
已知函数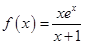 (
(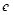 为自然对数的底数).
为自然对数的底数).
(1)若对任意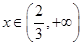 ,
,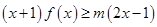 恒成立,求实数
恒成立,求实数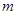 的取值范围;
的取值范围;
(2)设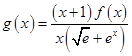 ,
, (
(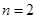 ,
,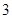 ,
,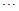 ).问:
).问:
是否存在正常数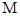 ,对任意给定的正整数
,对任意给定的正整数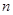 (
(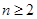 ),都有
),都有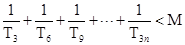 成立?若存在,
成立?若存在,
求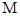 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
已知椭圆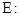
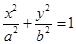 (
(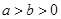 )的焦距为
)的焦距为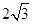 ,且经过点
,且经过点 .
.
(1)求椭圆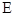 的标准方程;
的标准方程;
(2)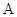 是椭圆
是椭圆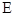 与
与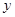 轴正半轴的交点,椭圆
轴正半轴的交点,椭圆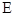 上是否存在两点
上是否存在两点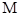 、
、 ,使得
,使得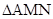 是以
是以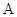 为直角顶
为直角顶
点的等腰直角三角形?若存在,请说明有几个;若不存在,请说明理由.
已知数列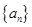 的前
的前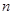 项和为
项和为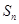 ,且
,且 .
.
(1)求数列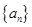 的通项公式;
的通项公式;
(2)若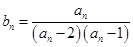 ,数列
,数列 的前
的前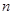 项和为
项和为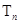 ,证明:
,证明: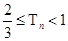 .
.
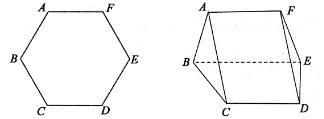
如图,将边长为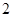 的正六边形
的正六边形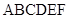 沿对角线
沿对角线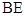 翻折,连接
翻折,连接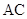 、
、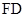 ,形成如图所示的多面体,且
,形成如图所示的多面体,且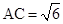 .
.
(1)证明:平面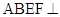 平面
平面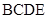 ;
;
(2)求平面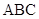 与平面
与平面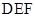 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值.
某中学一名数学老师对全班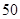 名学生某次考试成绩分男女生进行了统计(满分
名学生某次考试成绩分男女生进行了统计(满分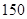 分),其中
分),其中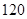 分(含
分(含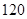 分)以上为优秀,绘制了如下的两个频率分布直方图:
分)以上为优秀,绘制了如下的两个频率分布直方图: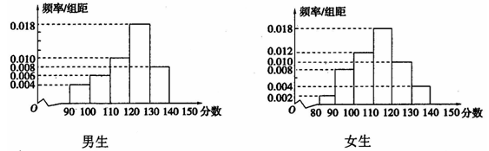
(1)根据以上两个直方图完成下面的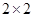 列联表:
列联表: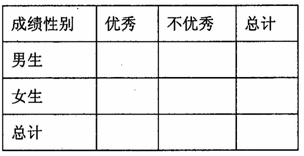
(2)根据(1)中表格的数据计算,你有多大把握认为学生的数学成绩与性别之间有关系?
附: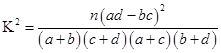 ,其中
,其中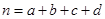 为样本容量
为样本容量
(3)若从成绩在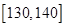 的学生中任取
的学生中任取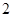 人,求取到的
人,求取到的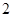 人中至少有
人中至少有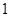 名女生的概率.
名女生的概率.