已知等差数列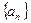 的前4项的和为8,且
的前4项的和为8,且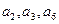 成等比数列。
成等比数列。
(1) 求通项公式
(2)令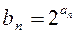 ,求数列
,求数列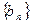 的前n项之和
的前n项之和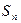
如图,在平面直角坐标系 中,椭圆
中,椭圆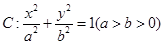 的离心率为
的离心率为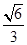 ,直线
,直线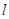 与
与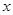 轴交于点
轴交于点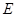 ,与椭圆
,与椭圆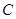 交于
交于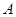 、
、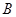 两点.当直线
两点.当直线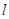 垂直于
垂直于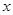 轴且点
轴且点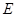 为椭圆
为椭圆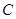 的右焦点时, 弦
的右焦点时, 弦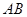 的长为
的长为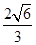 .
.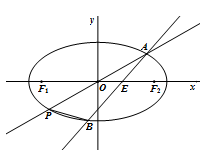
(1)求椭圆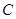 的方程;
的方程;
(2)若点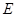 的坐标为
的坐标为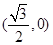 ,点
,点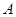 在第一象限且横坐标为
在第一象限且横坐标为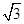 ,连结点
,连结点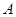 与原点
与原点 的直线交椭圆
的直线交椭圆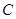 于另一点
于另一点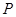 ,求
,求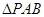 的面积;
的面积;
(3)是否存在点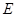 ,使得
,使得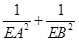 为定值?若存在,请指出点
为定值?若存在,请指出点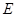 的坐标,并求出该定值;若不存在,请说明理由.
的坐标,并求出该定值;若不存在,请说明理由.
如图,在三棱锥 中,
中,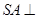 底面
底面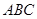 ,
,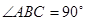 ,且
,且 ,点
,点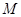 是
是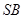 的中点,
的中点, 且交
且交 于点
于点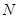 .
.
(1)求证: 平面
平面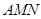 ;
;
(2)当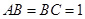 时,求三棱锥
时,求三棱锥 的体积.
的体积.
2015年8月12日天津发生危化品重大爆炸事故,造成重大人员和经济损失.某港口组织消防人员对该港口的公司的集装箱进行安全抽检,已知消防安全等级共分为四个等级(一级为优,二级为良,三级为中等,四级为差),该港口消防安全等级的统计结果如下表所示:
| 等 级 |
一级 |
二级 |
三级 |
四级 |
| 频 率 |
0.30 |
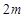 |
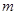 |
0.10 |
现从该港口随机抽取了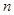 家公司,其中消防安全等级为三级的恰有20家.
家公司,其中消防安全等级为三级的恰有20家.
(1)求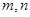 的值;
的值;
(2)按消防安全等级利用分层抽样的方法从这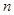 家公司中抽取10家,除去消防安全等级为一级和四级的公司后,再从剩余公司中任意抽取2家,求抽取的这2家公司的消防安全等级都是二级的概率.
家公司中抽取10家,除去消防安全等级为一级和四级的公司后,再从剩余公司中任意抽取2家,求抽取的这2家公司的消防安全等级都是二级的概率.
设数列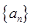 的前
的前 项和为
项和为 ,数列
,数列 为等比数列,且
为等比数列,且 .
.
(1)求数列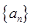 和
和 的通项公式;
的通项公式;
(2)设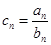 ,求数列
,求数列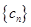 的前
的前 项和
项和 .
.
已知函数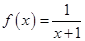 ,点
,点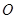 为坐标原点, 点
为坐标原点, 点 N
N ,向量
,向量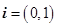 ,
,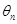 是向量
是向量 与
与 的夹角,则
的夹角,则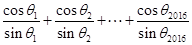 的值为 .
的值为 .