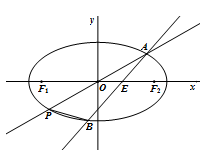
如图,在平面直角坐标系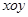 中,椭圆
中,椭圆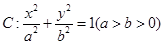 的离心率为
的离心率为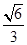 ,直线
,直线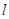 与
与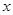 轴交于点
轴交于点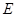 ,与椭圆
,与椭圆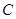 交于
交于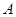 、
、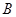 两点.当直线
两点.当直线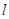 垂直于
垂直于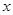 轴且点
轴且点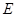 为椭圆
为椭圆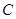 的右焦点时, 弦
的右焦点时, 弦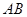 的长为
的长为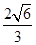 .
.
(1)求椭圆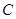 的方程;
的方程;
(2)若点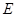 的坐标为
的坐标为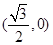 ,点
,点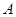 在第一象限且横坐标为
在第一象限且横坐标为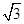 ,连结点
,连结点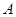 与原点
与原点 的直线交椭圆
的直线交椭圆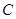 于另一点
于另一点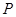 ,求
,求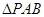 的面积;
的面积;
(3)是否存在点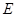 ,使得
,使得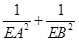 为定值?若存在,请指出点
为定值?若存在,请指出点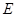 的坐标,并求出该定值;若不存在,请说明理由.
的坐标,并求出该定值;若不存在,请说明理由.
选修4—4:坐标系与 参数方程。
参数方程。
在平面直角坐标系xOy中,已知曲线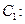
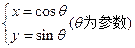 ,以平面直角坐标系xOy
,以平面直角坐标系xOy
的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线 .
.
(1)将曲线 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的 、2倍后得到曲线
、2倍后得到曲线 试写出直线
试写出直线 的直角坐标方程和曲线
的直角坐标方程和曲线 的参数方程;
的参数方程;
(2)在曲线 上求一点P,使点P到直线
上求一点P,使点P到直线 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
选修4-1:几何证明选讲
如图所示,已知PA与⊙O相切,A为切点,PBC为割线,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF·EC.
(1)求证:ÐP=ÐEDF;
(2)求证:CE·EB=EF·EP.
(本小题满分12分)已知二次函数f(x)=ax2+bx+c.
(1)若f(-1)=0,试判断函数f(x)零点的个数;
(2)是否存在a,b,c∈R,使f(x)同时满足以下条件:
①对任意x∈R,f(-1+x)=f(-1-x),且f(x)≥0;
②对任意x∈R,都有0≤f(x)-x≤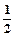 (x-1)2.若存在,求出a,b,c的值;若不存在,请说
(x-1)2.若存在,求出a,b,c的值;若不存在,请说
明理由。
(3)若对任意x1、x2∈R且x1<x2,f(x1)≠f(x2),试证明:存在x0∈(x1,x2),使f(x0)=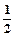 [f(x1)+f(x2)]成立。
[f(x1)+f(x2)]成立。
(本小题满分12分)
函数f(x)=x2-2x+2在闭区间[t,t+1](t∈R)上的最小值为g(t).
(1)试写出g(t)的表达式;
(2)作g(t)的图象并写出g(t)的最小值。
(本小题满分12分)
设函数f(x)=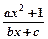 是奇函数(a,b,c都是整数)且f(1)=2,f(2)<3
是奇函数(a,b,c都是整数)且f(1)=2,f(2)<3
(1)求a,b,c的值;
(2)当x<0,f(x)的单调性如何?用单调性定义证明你的结论。
(3)当x>0时,求函数f(x)的最小值。