如图,已知正方形 的边长为1,
的边长为1, 平面
平面 ,
,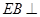 平面
平面 ,
,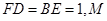 为
为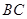 边上的动点。
边上的动点。
(1)证明: 平面
平面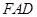 ;
;
(2)试探究点 的位置,使平面
的位置,使平面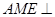 平面
平面 。
。
已知矩阵A=,若矩阵A属于特征值6的一个特征向量为α1=,属于特征值1的一个特征向
量为α2=.求矩阵A,并写出A的逆矩阵.
已知数列 为等差数列,
为等差数列, ,
, 的前
的前 和为
和为 ,数列
,数列 为等
为等
比数列,且 对任意的
对任意的 恒成立.
恒成立.
(Ⅰ)求数列 、
、 的通项公式;
的通项公式;
(Ⅱ)是否存在非零整数 ,使不等式
,使不等式 对一切
对一切 都成立?若存在,求出
都成立?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(Ⅲ)各项均为正整数的无穷等差数列 ,满足
,满足 ,且存在正整数k,使
,且存在正整数k,使 成等比数列,若数列
成等比数列,若数列 的公差为d,求d的所有可能取值之和.
的公差为d,求d的所有可能取值之和.
设函数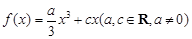 .
.
(Ⅰ)若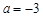 ,函数
,函数 在
在 的值域为
的值域为 ,求函数
,求函数 的零点;
的零点;
(Ⅱ)若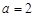 ,
,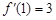 ,
, .
.
(1)对任意的 ,
, 恒成立, 求实数
恒成立, 求实数 的最小值;
的最小值;
(2)令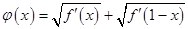 ,若存在
,若存在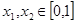 使得
使得 ,求实数
,求实数 的取值范围.
的取值范围.
如图,在平面直角坐标系xOy中,已知椭圆 :
: 的
的
离心率为 ,且右焦点F到左准线l的距离为
,且右焦点F到左准线l的距离为 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)(1)设椭圆 上的任一点
上的任一点 ,从原点
,从原点 向圆
向圆 引两条
引两条
切线,设两条切线的斜率分别为 ,当
,当 为定值时求
为定值时求 的值;
的值;
(2)在(1)的条件下,当两条切线分别交椭圆于 时,试探究
时,试探究 是否为定值,若是,求出其值;若不是,请说明理由.
是否为定值,若是,求出其值;若不是,请说明理由.
某油库的设计容量为30万吨,年初储量为10万吨,从年初起计划每月购
进石油 万吨,以满足区域内和区域外的需求,若区域内每月用石油1万吨,区域外前
万吨,以满足区域内和区域外的需求,若区域内每月用石油1万吨,区域外前 个月的需求总量
个月的需求总量 (万吨)与
(万吨)与 的函数关系为
的函数关系为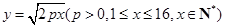 ,若区域外前4个月的需求总量为20万吨.
,若区域外前4个月的需求总量为20万吨.
(Ⅰ)试求出当第 个月的石油调出后,油库内储油量
个月的石油调出后,油库内储油量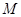 (万吨)与
(万吨)与 的函数关系式;
的函数关系式;
(Ⅱ)要使16个月内每月按计划购进石油之后,油库总能满足区域内和区域外的需求,且每月石油调出后,油库的石油剩余量不超过油库的容量,试确定 的取值范围.
的取值范围.