(本小题满分12分)
如图,点 是椭圆
是椭圆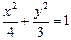 上一动点,点
上一动点,点 是点
是点 在
在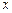 轴上的射影,坐标平面
轴上的射影,坐标平面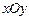 内动点
内动点 满足:
满足: (
(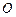 为坐标原点),设动点
为坐标原点),设动点 的轨迹为曲线
的轨迹为曲线 .
.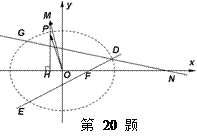
(Ⅰ)求曲线 的方程并画出草图;
的方程并画出草图;
(Ⅱ)过右焦点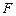 的直线
的直线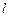 交曲线
交曲线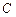 于
于 ,
, 两点,且
两点,且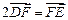 ,点
,点 关于
关于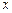 轴的对称点为
轴的对称点为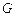 ,求直线
,求直线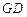 的方程.
的方程.
已知 ,且
,且 .
.
(1)求 的值;
的值;
(2)求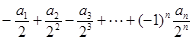 的值.
的值.
在数列 中,
中, ,且前
,且前 项的算术平均数等于第
项的算术平均数等于第 项的
项的 倍(
倍( )。
)。
(1)写出此数列的前5项;(2)归纳猜想 的通项公式,并加以证明。
的通项公式,并加以证明。
已知函数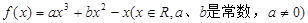 ,且当
,且当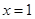 及
及 时取得极值。
时取得极值。
(1)求函数 的解析式;
的解析式;
(2)若曲线 与
与 有两个不同的交点,求实数
有两个不同的交点,求实数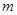 的取值范围.
的取值范围.
统计表明,某种型号的汽车在匀速行驶中每小时的耗油量y (升)关于行驶速度x (千米/小时)的函数解析式可以表示为: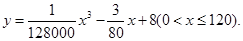 已知甲、乙两地相距100千米。
已知甲、乙两地相距100千米。
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
已知二次函数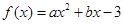 在
在 处取得极值,且在
处取得极值,且在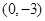 点处的切线与直线
点处的切线与直线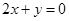 平行。
平行。
(1)求 的解析式;
的解析式;
(2)求函数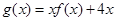 的单调递增区间及极值;
的单调递增区间及极值;
(3)求函数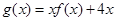 在
在 的最值。
的最值。