设
分别是椭圆
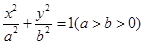的左右焦点,若在其右准线上存在点
,使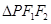
为等腰三角形,则椭圆的离心率的取值范围是（ ）
A． |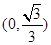
B． |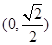
C． |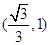
D． |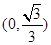
分析法又称执果索因法，若用分析法证明：“设a＞b＞c，且a+b+c=0”，求证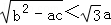
”索的因应是（）
| A．a﹣b＞0 |
| B．a﹣c＞0 |
| C．（a﹣b）（a﹣c）＞0 |
| D．（a﹣b）（a﹣c）＜0 |
命题“对于任意角θ，cos4θ﹣sin4θ=cos2θ”的证明：“cos4θ﹣sin4θ=（cos2θ﹣sin2θ）（cos2θ+sin2θ）=cos2θ﹣sin2θ=cos2θ”过程应用了（）
| A．分析发 |
| B．综合法 |
| C．综合法、分析法结合使用 |
| D．间接证法 |
若P=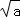
+
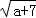，Q=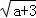
+
（a≥0），则P，Q的大小关系是（）
| A．P＞Q | B．P=Q | C．P＜Q | D．由a的取值确定 |
分析法是从要证的不等式出发，寻求使它成立的（）
| A．充分条件 | B．必要条件 |
| C．充要条件 | D．既不充分又不必要条件 |
证明命题：“f（x）=ex+
在（0，+∞）上是增函数”，现给出的证法如下：
因为f（x）=ex+，所以f′（x）=ex﹣，
因为x＞0，所以ex＞1，0＜＜1，
所以ex﹣＞0，即f′（x）＞0，
所以f（x）在（0，+∞）上是增函数，使用的证明方法是（）
| A．综合法 | B．分析法 | C．反证法 | D．以上都不是 |