设函数 ,其中
,其中 。
。
(1)当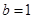 时,
时,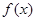 在
在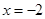 时取得极值,求
时取得极值,求 ;
;
(2)当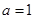 时,若
时,若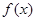 在
在 上单调递增,求
上单调递增,求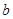 的取值范围;
的取值范围;
(3)证明对任意的正整数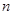 ,不等式
,不等式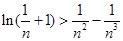 都成立。
都成立。
数列{an}中,a1=3,an+1=an+cn(c是常数,n=1,2,3,…),且a1,a2,a3成公比不为1的等比数列.
(1)求c的值;
(2)求数列{an}的通项公式.
在数列{an}和等比数列{bn}中,a1=0,a3=2,bn=2an+1(n∈N*).
(1)求数列{bn}及{an}的通项公式;
(2)若cn=an·bn,求数列{cn}的前n项和Sn.
已知各项均为正数的等比数列{an}的首项a1=2,Sn为其前n项和,若5S1,S3,3S2成等差数列.
(1)求数列{an}的通项公式;
(2)设bn=log2an,cn=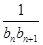 ,记数列{cn}的前n项和Tn.若对n∈N*,Tn≤k(n+4)恒成立,求实数k的取值范围.
,记数列{cn}的前n项和Tn.若对n∈N*,Tn≤k(n+4)恒成立,求实数k的取值范围.
已知数列{an}满足a1=1,an-an-1+2anan-1=0(n∈N*,n>1).
(1)求证:数列 是等差数列并求数列{an}的通项公式;
是等差数列并求数列{an}的通项公式;
(2)设bn=anan+1,求证:b1+b2+…+bn< 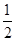 .
.
等差数列{an}中,a3=3,a1+a4=5.
(1)求数列{an}的通项公式;
(2)若bn= ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.