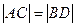(本小题满分12分)(1)已知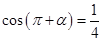 ,
,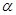 为第二象限角,求
为第二象限角,求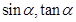 ;
;
(2)当 ,求
,求 的值。
的值。
(本小题满分12分)某中学生物兴趣小组在学校生物园地种植了一批名贵树苗,为了解树苗的生长情况,从这批树苗中随机地测量了其中50棵树苗的高度(单位:厘米),并把这些高度列成了如下的频数分布表:
(1)在这批树苗中任取,其高度在85厘米以上的大约有多少棵;
(2)这批树苗的平均 高度大约是多少?(计算时可以用组中值代替各组数据的平均值);
高度大约是多少?(计算时可以用组中值代替各组数据的平均值);
(3)为了进一步获得研究资料,若从 组中移出一棵树苗,从
组中移出一棵树苗,从 组中移出两棵树苗进行试验研究,则
组中移出两棵树苗进行试验研究,则 组中的树苗A和
组中的树苗A和 组中的树苗C同时被移出的概率是多少?
组中的树苗C同时被移出的概率是多少?
给出命题p:  ;命题q:曲线
;命题q:曲线 与
与 轴交于不同的两点.
轴交于不同的两点. 如果命题“
如果命题“ ”为真,“
”为真,“ ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.
已知在平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为 ,且过
,且过 ,设点
,设点 .
.
(1)求该椭圆的标准方程;
(2)若 是椭圆上的动点,求线段
是椭圆上的动点,求线段 中点
中点 的轨迹方程;
的轨迹方程;
(本小题满分12分)
(1)写出命题“若 是偶数,则
是偶数,则 是偶数”的否命题;并对否命题的真假给予说明。
是偶数”的否命题;并对否命题的真假给予说明。
(2)求证:“ ”是“方程
”是“方程 无实根”的必要不充分条件。
无实根”的必要不充分条件。
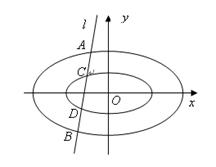
(本小题满分14分)定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”。如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比。已知椭圆 。
。
(1)若椭圆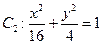 ,判断
,判断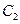 与
与 是否相似?如果相似,求出
是否相似?如果相似,求出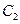 与
与 的相似比;如果不相似,请说明理由;
的相似比;如果不相似,请说明理由;
(2)写出与椭圆 相似且短半轴长为
相似且短半轴长为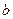 的椭圆
的椭圆 的方程;若在椭圆
的方程;若在椭圆 上存在两点
上存在两点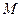 、
、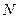 关于直线
关于直线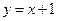 对称,求实数
对称,求实数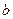 的取值范围?
的取值范围?
(3)如图:直线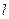 与两个“相似椭圆”
与两个“相似椭圆”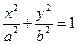 和
和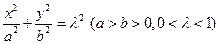 分别交于点
分别交于点 和点
和点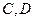 ,证明:
,证明: