(本小题满分14分)定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”。如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比。已知椭圆 。
。
(1)若椭圆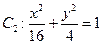 ,判断
,判断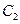 与
与 是否相似?如果相似,求出
是否相似?如果相似,求出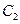 与
与 的相似比;如果不相似,请说明理由;
的相似比;如果不相似,请说明理由;
(2)写出与椭圆 相似且短半轴长为
相似且短半轴长为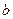 的椭圆
的椭圆 的方程;若在椭圆
的方程;若在椭圆 上存在两点
上存在两点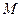 、
、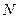 关于直线
关于直线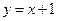 对称,求实数
对称,求实数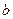 的取值范围?
的取值范围?
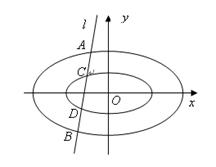
(3)如图:直线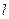 与两个“相似椭圆”
与两个“相似椭圆”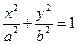 和
和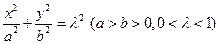 分别交于点
分别交于点 和点
和点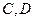 ,证明:
,证明: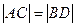
某校积极响应《全面健身条例》,把周五下午5:0 0~6:00定为职工活动时间,并成立了行政和教师两支篮球队,但由于工作性质所限,每月(假设为4周)每支球队只能组织两次活动,且两支球队的活动时间是相互独立的。
0~6:00定为职工活动时间,并成立了行政和教师两支篮球队,但由于工作性质所限,每月(假设为4周)每支球队只能组织两次活动,且两支球队的活动时间是相互独立的。
(1)求这两 支球队每月两次都在同一时间活动的频率;
支球队每月两次都在同一时间活动的频率;
(2)设这两支球队每月能同时活动的次数为 ,求随机变量
,求随机变量 的分布列和数学期望。
的分布列和数学期望。
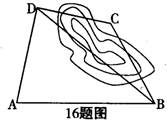 如图,为了计算渭河岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两个测量点,现测得AD⊥CD,AD=100m,AB=140m,∠BDA=60°,∠BCD=135°,求两景点B与C的距离(假设A,B,C,D在同一平面内,测量结果保留整数;参考数据:
如图,为了计算渭河岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两个测量点,现测得AD⊥CD,AD=100m,AB=140m,∠BDA=60°,∠BCD=135°,求两景点B与C的距离(假设A,B,C,D在同一平面内,测量结果保留整数;参考数据: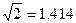 ,
, ,
, .)
.)

 设△ABC的内角A、B、C的对边长分别为a、b、c,
设△ABC的内角A、B、C的对边长分别为a、b、c,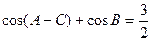 ,
,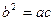 ,求B.
,求B.
函数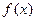 的定义域为
的定义域为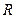 ,并满足条件
,并满足条件
①对任意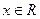 ,有
,有 ;
;
②对任意 ,有
,有 ;
;
③ .
.
(1)求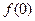 的值;
的值; (2)求证:
(2)求证: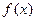 在
在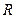 上是单调递增函数;
上是单调递增函数;
(3)若 ,且
,且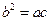 ,求证
,求证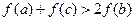 .
.
已知直线 与曲线
与曲线
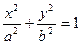
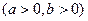 交于不同的两点
交于不同的两点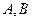 ,
,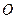 为坐标原点.
为坐标原点.
(Ⅰ)若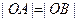 ,求证:曲线
,求证:曲线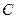 是一个圆;
是一个圆;
(Ⅱ)若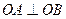 ,当
,当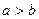 且
且 时,求曲线
时,求曲线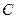 的离心率
的离心率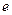 的取值范围.
的取值范围.