对于数列 ,如果存在一个正整数
,如果存在一个正整数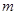 ,使得对任意的
,使得对任意的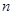 (
( )都有
)都有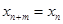 成立,那么就把这样一类数列
成立,那么就把这样一类数列 称作周期为
称作周期为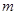 的周期数列,
的周期数列,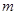 的最小值称作数列
的最小值称作数列 的最小正周期,以下简称周期.例如当
的最小正周期,以下简称周期.例如当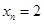 时
时 是周期为
是周期为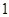 的周期数列,当
的周期数列,当 时
时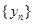 是周期为
是周期为 的周期数列.
的周期数列.
(1)设数列 满足
满足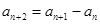 (
( ),
),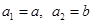 (
(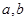 不同时为0),求证:数列
不同时为0),求证:数列 是周期为
是周期为 的周期数列,并求数列
的周期数列,并求数列 的前2012项的和
的前2012项的和 ;
;
(2)设数列 的前
的前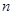 项和为
项和为 ,且
,且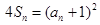 .
.
①若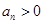 ,试判断数列
,试判断数列 是否为周期数列,并说明理由;
是否为周期数列,并说明理由;
②若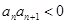 ,试判断数列
,试判断数列 是否为周期数列,并说明理由;
是否为周期数列,并说明理由;
(3)设数列 满足
满足 (
( ),
), ,
,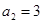 ,数列
,数列 的前
的前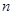 项和为
项和为 ,试问是否存在实数
,试问是否存在实数 ,使对任意的
,使对任意的 都有
都有 成立,若存在,求出
成立,若存在,求出 的取值范围
的取值范围 ;不存在,说明理由.
;不存在,说明理由.
某宾馆有客房300间,每间日房租为100元时,每天都客满,宾馆欲提高档次,并提高租金,如果每间日房租每增加10元,客房出租数就会减少10间,若不考虑其他因素,该宾馆将房间租金提高到多少元时,每天客房的租金总收入最高,并求出日租金的最大值?
已知函数f(x)=alnx+bx,且f(1)=-1,f′(1)=0,
⑴求f(x);
⑵求f(x)的最大值;
⑶若x>0,y>0,证明:lnx+lny≤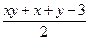 .
.
已知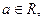 函数
函数 .
.
(Ⅰ)当a=3时,求f(x)的零点;
(Ⅱ)求函数y=f (x)在区间 [ 1,2 ] 上的最小值.
已知函数 .
.
(Ⅰ)若 在
在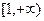 上是增函数,求实数a的取值范围.
上是增函数,求实数a的取值范围.
(Ⅱ)若 是
是 的极大值点,求
的极大值点,求 在
在 上的最大值;
上的最大值;
(Ⅲ)在(2)的条件下,是否存在实数b,使得函数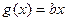 的图像与函数
的图像与函数 的图像恰有3个交点,若存在,求出b的取值范围,若不存在,说明理由.
的图像恰有3个交点,若存在,求出b的取值范围,若不存在,说明理由.
设函数
,已知
和
为
的极值点.
(Ⅰ)求
和
的值;
(Ⅱ)讨论函数
的单调性;
(Ⅲ)设
,比较
与
的大小.