抛掷A,B,C三枚质地不均匀的纪念币,它们正面向上的概率如下表所示 ;
;
| 纪念币 |
A |
B |
C |
| 概率 |
 |
a |
a |
将这三枚纪念币同时抛掷一次,设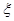 表示出现正面向上的纪念币的个数。
表示出现正面向上的纪念币的个数。
(1)求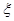 的分布列及数学期
的分布列及数学期 望;
望;
(2)在概率 中,若
中,若 的值最大,求a的最大值。
的值最大,求a的最大值。
在极坐标系中,曲线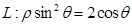 ,过点A(5,α)(α为锐角且
,过点A(5,α)(α为锐角且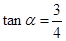 )作平行于
)作平行于 的直线
的直线 ,且
,且 与曲线L分别交于B,C两点。
与曲线L分别交于B,C两点。
(1)以极点为原点,极轴为x轴的正半轴,取与极坐标相同单位长度,建立平面直角坐标系,写出曲线L和直线 的普通方程;
的普通方程;
(2)求|BC|的长。
如图,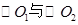 相交于A、B两点,AB是
相交于A、B两点,AB是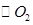 的直径,过A点作
的直径,过A点作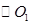 的切线交
的切线交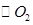 于点E,并与BO1的延长线交于点P,PB分别与
于点E,并与BO1的延长线交于点P,PB分别与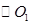 、
、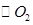 交于C,D两点。
交于C,D两点。
求证:(1)PA·PD=PE·PC;
(2)AD=AE。
如图,F1,F2是离心率为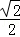 的椭圆C:
的椭圆C: (a>b>0)的左、右焦点,直线l:x=﹣
(a>b>0)的左、右焦点,直线l:x=﹣ 将线段F1F2分成两段,其长度之比为1:3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.
将线段F1F2分成两段,其长度之比为1:3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.
(1)求椭圆C的方程;
(2)求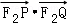 的取值范围.
的取值范围.
已知数列{an}中,a1=1,an>0,an+1是函数f(x)= x3+
x3+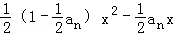 的极小值点.
的极小值点.
(1)证明数列{an}为等比数列,并求出通项公式an;
(2)设bn=nan2,数列{bn}的前n项和为Sn,求证: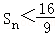 .
.
某品牌的汽车4S店,对最近100位采用分期付款的购车者进行统计,统计结果如右表所示:已知分3期付款的频率为0.2,4S店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款其利润为1.5万元;分4期或5期付款,其利润为2万元.用η表示经销一辆汽车的利润.
(1)求上表中的a,b值;
(2)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有1位采用3期付款”的概率P(A);
(3)求η的分布列及数学期望Eη.