(本小题满分14分)已知数列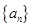 的前
的前 项和
项和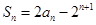 .
.
(1)证明:数列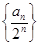 是等差数列;
是等差数列;
(2)若不等式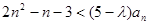 对
对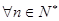 恒成立,求
恒成立,求 的取值范围.
的取值范围.
已知两个不共线的向量 ,它们的夹角为
,它们的夹角为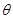 ,且
,且 ,
,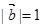 ,
,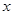 为正实数.
为正实数.
(1)若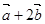 与
与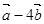 垂直,求
垂直,求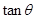 ;
;
(2)若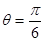 ,求
,求 的最小值及对应的
的最小值及对应的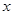 的值,并判断此时向量
的值,并判断此时向量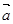 与
与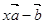 是否垂直?
是否垂直?
已知函数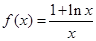 .
.
(1)若函数 在区间
在区间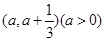 上存在极值点,求实数
上存在极值点,求实数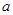 的取值范围;
的取值范围;
(2)当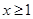 时,不等式
时,不等式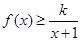 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)求证: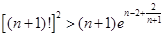 .(
.(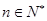 ,
, 为自然对数的底数)
为自然对数的底数)
已知椭圆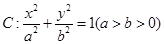 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线 相切,直线
相切,直线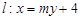 与椭圆C相交于A、B两点.
与椭圆C相交于A、B两点.
(1)求椭圆C的方程;(2)求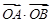 的取值范围;
的取值范围;
单调递增数列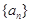 的前
的前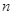 项和为
项和为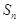 ,且满足
,且满足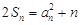 ,
,
(1)求数列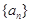 的通项公式;
的通项公式;
(2)数列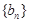 满足
满足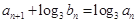 ,求数列
,求数列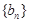 的前
的前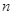 项和
项和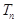 .
.