求下列各式的值: (1)
(1)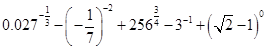
 (2)
(2)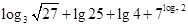
函数 的图象如下图所示.
的图象如下图所示.
(1)求解析式中 的值;
的值;
(2)该图像可由 的图像先向_____(填“左”或“右”)平移_______个单位,
的图像先向_____(填“左”或“右”)平移_______个单位,
再横向拉伸到原来的_______倍.纵向拉伸到原来的______倍得到.
已知 ,
,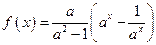 .
.
(1)判断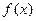 的奇偶性并加以证明;
的奇偶性并加以证明;
(2)判断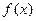 的单调性并用定义加以证明;
的单调性并用定义加以证明;
(3)当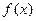 的定义域为
的定义域为 时,解关于m的不等式
时,解关于m的不等式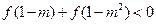 .
.
探究函数 的图像时,.列表如下:
的图像时,.列表如下:
| x |
… |
0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
| y |
… |
8.5 |
5 |
4.17 |
4.05 |
4.005 |
4 |
4.005 |
4.02 |
4.04 |
4.3 |
5 |
5.8 |
7.57 |
… |
观察表中y值随x值的变化情况,完成以下的问题:
⑴函数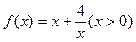 的递减区间是 ,递增区间是 ;
的递减区间是 ,递增区间是 ;
⑵若对任意的 恒成立,试求实数m的取值范围.
恒成立,试求实数m的取值范围.
已知实数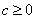 ,曲线
,曲线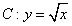 与直线
与直线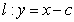 的交点为
的交点为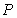 (异于原点
(异于原点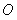 ),在曲线
),在曲线 上取一点
上取一点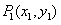 ,过点
,过点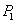 作
作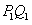 平行于
平行于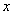 轴,交直线
轴,交直线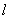 于点
于点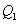 ,过点
,过点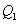 作
作 平行于
平行于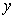 轴,交曲线
轴,交曲线 于点
于点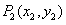 ,接着过点
,接着过点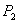 作
作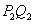 平行于
平行于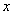 轴,交直线
轴,交直线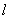 于点
于点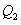 ,过点
,过点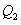 作
作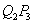 平行于
平行于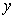 轴,交曲线
轴,交曲线 于点
于点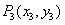 ,如此下去,可以得到点
,如此下去,可以得到点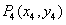 ,
,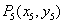 ,…,
,…,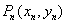 ,… .设点
,… .设点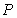 的坐标为
的坐标为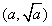 ,
,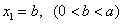 .
.
(Ⅰ)试用 表示
表示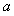 ,并证明
,并证明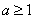 ;
;
(Ⅱ)试证明 ,且
,且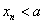 (
(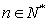 );
);
(Ⅲ)当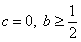 时,求证:
时,求证: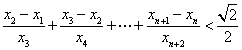 (
(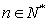 ).
).
如下图所示,在直角坐标系 中,射线
中,射线 在第一象限,且与
在第一象限,且与 轴的正半轴成定角
轴的正半轴成定角 ,动点
,动点 在射线
在射线 上运动,动点
上运动,动点 在
在 轴的正半轴上运动,
轴的正半轴上运动, 的面积为
的面积为 .
.
(Ⅰ)求线段 中点
中点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ) 是曲线
是曲线 上的动点,
上的动点,  到
到 轴的距离之和为
轴的距离之和为 ,
,
设 为
为 到
到 轴的距离之积.问:是否存在最大的常数
轴的距离之积.问:是否存在最大的常数 ,
,
使 恒成立?若存在,求出这个
恒成立?若存在,求出这个 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.