.如图直角梯形OABC中,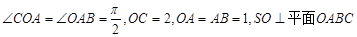 ,
,
SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
(Ⅰ)求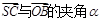 的余弦值;
的余弦值;
(Ⅱ)设
①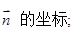
②设OA与平面SBC所成的角为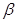 ,求
,求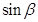 。
。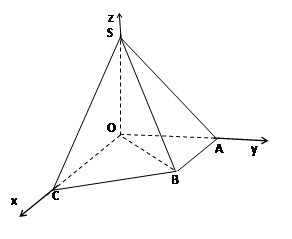
已知函数f(x)=Asin(x+φ)(A>0,0<φ<π)(x∈R)的最大值是1,其图象经过点M.
(1)求f(x)的解析式;
(2)已知α、β∈,且f(α)=,f(β)=,
求f(α-β)的值.
已知数列{an}满足,a1=1,a2=2,an+2=,n∈N.
(1)令bn=an+1-an,证明:{bn}是等比数列:
(2)求{an}的通项公式.
设曲线y=x2+x+1-ln x在x=1处的切线为l,数列{an}中,a1=1,且点(an,an+1)在切线l上.
(1)求证:数列{1+an}是等比数列,并求an;
(2)求数列{an}的前n项和Sn.
等比数列{an}的前n项和为Sn,已知S1,S3,S2成等差数列.
(1)求{an}的公比q;
(2)若a1-a3=3,求Sn,
等比数列{an}中,已知a1=2,a4=16.
(1)求数列{an}的通项公式;
(2)若a3,a5分别为等差数列{bn}的第3项和第5项,试求数列{bn}的通项公式及前n项和Sn.