(本小题满分14分)
一个四棱锥的三视图如图所示,E为侧棱PC上一动点。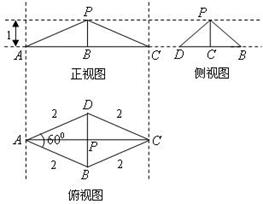
(1)画出该四棱锥的直观图,并指出几何体的主要特征(高、底等).
(2)点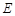 在何处时,
在何处时, 面EBD,并求出此时二面角
面EBD,并求出此时二面角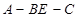 平面角的余弦值.
平面角的余弦值.
(本小题满分14分)
已知向量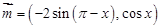 ,
, ,函数
,函数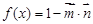 .
.
(1)求函数 的解析式;
的解析式;
(2)当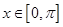 时,求
时,求 的单调递增区间;
的单调递增区间;
(3)说明 的图象可以由
的图象可以由 的图象经过怎样的变换而得到.
的图象经过怎样的变换而得到.
.(本小题满分12分)
已知集合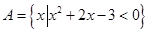 ,
, ,
,
(1)在区间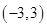 上任取一个实数
上任取一个实数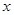 ,求“
,求“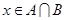 ”的概率;
”的概率;
(2)设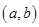 为有序实数对,其中
为有序实数对,其中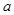 是从集合
是从集合 中任取的一个整数,
中任取的一个整数,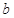 是从集合
是从集合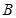 中任取的一个整数,求“
中任取的一个整数,求“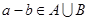 ”的概率.
”的概率.
、(本小题满分14分)设函数
(Ⅰ)求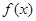 的单调区间;
的单调区间;
(Ⅱ)当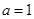 时,若方程
时,若方程 在
在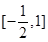 上有两个实数解,求实数t的取值范围;
上有两个实数解,求实数t的取值范围;
(Ⅲ)证明:当m>n>0时,
(本小题满分14分) 已知数列 满足:
满足:
(Ⅰ)探究数列 是等差数列还是等比数列,并由此求数列
是等差数列还是等比数列,并由此求数列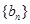 的通项公式;
的通项公式;
(Ⅱ)求数列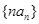 的前n项和
的前n项和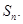
(本小题满分14分)
已知汕头市某学校高中部某班共有学生50人,其中男生30人,女生20人,班主任决定用分层抽样的方法在自己班上的学生中抽取5人进行高考前心理调查。
(Ⅰ)若要从这5人中选取2人作为重点调查对象,求至少选取1个男生的概率;
(Ⅱ)若男学生考前心理状态好的概率为0.6,女学生考前心理状态好的概率为0.5, 表示抽取的5名学生中考前心理状态好的人数,求P(
表示抽取的5名学生中考前心理状态好的人数,求P( =1)及E
=1)及E .
.