已知极坐标系的极点在直角坐标系的原点处,极轴与 轴的正半轴重合.
轴的正半轴重合.
直线 的参数方程为:
的参数方程为: (t为参数),曲线
(t为参数),曲线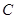 的极坐标方程为:
的极坐标方程为: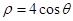 .
.
(Ⅰ)写出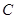 的直角坐标方程,并指出
的直角坐标方程,并指出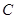 是什么曲线;
是什么曲线;
(Ⅱ)设直线 与曲线
与曲线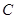 相交于
相交于 、
、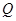 两点,求
两点,求 值.
值.
已知向量a=(3sinα,cosα),b=(2sinα, 5sinα-4cosα),α∈( ),且a⊥b. 求tanα的值;
),且a⊥b. 求tanα的值;
设函数f(x)= x3-mx2+(m2-4)x,x∈R.
(1)当m=3时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)已知函数f(x)有三个互不相同的零点0,α,β,且α<β.若对任意的
x∈[α,β],都有f(x)≥f(1) 恒成立,求实数m的取值范围.
某投资公司投资甲、乙两个项目所获得的利润分别是P(亿元)和Q(亿元),它们与投资额t(亿元)的关系有经验公式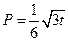 ,
, .今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元).
.今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元).
求:(1)y关于x的函数表达式;
(2)总利润的最大值.
如图,四棱锥P—ABCD中,四边形ABCD为矩形,平面PAD⊥平面ABCD,且E、O分别为PC、BD的中点.
求证:(1)EO∥平面PAD;
(2)平面PDC⊥平面PAD.
|
已知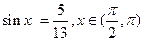 ,求cos2x和
,求cos2x和 值.
值.