如图,四棱锥P—ABCD中,四边形ABCD为矩形,平面PAD⊥平面ABCD,且E、O分别为PC、BD的中点.

求证:(1)EO∥平面PAD;
(2)平面PDC⊥平面PAD.
|
某出版社新出版一本高考复习用书,该书的成本为5元/本,经销过程中每本书需付给代理商m元(1≤m≤3)的劳务费,经出版社研究决定,新书投放市场后定价为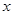 元/本(9≤
元/本(9≤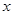 ≤11),预计一年的销售量为
≤11),预计一年的销售量为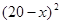 万本.
万本.
(1)求该出版社一年的利润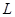 (万元)与每本书的定价
(万元)与每本书的定价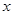 的函数关系式;
的函数关系式;
(2)当每本书的定价为多少元时,该出版社一年的利润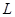 最大,并求出
最大,并求出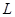 的最大值
的最大值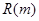 .
.
如图已知抛物线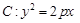 的焦点坐标为
的焦点坐标为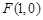 ,过
,过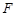 的直线交抛物线
的直线交抛物线 于
于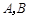 两点,直线
两点,直线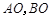 分别与直线
分别与直线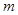 :
: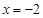 相交于
相交于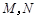 两点.
两点.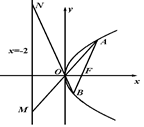
(1)求抛物线 的方程;
的方程;
(2)证明△ABO与△MNO的面积之比为定值.
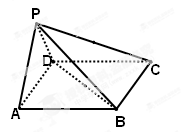
如图在四棱锥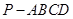 中,底面
中,底面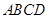 是边长为
是边长为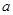 的正方形,侧面
的正方形,侧面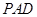
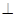 底面
底面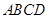 ,且
,且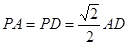 .
.
(1)求证:面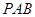
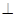 平面
平面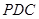 ;
;
(2)求二面角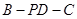 的余弦值.
的余弦值.
已知等差数列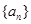 的首项
的首项 ,公差
,公差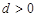 .且
.且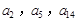 分别是等比数列
分别是等比数列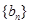 的
的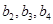 .
.
(1)求数列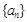 与
与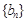 的通项公式;
的通项公式;
(2)设数列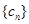 对任意自然数
对任意自然数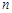 均有
均有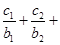
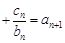 成立,求
成立,求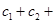
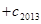 的值.
的值.
在△ABC中,角A,B,C的对边分别为a,b,c,且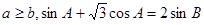 .
.
(1)求角C的大小;
(2)求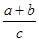 的最大值.
的最大值.