(本小题满分14分)
如图7,已知椭圆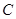 :
: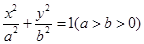 的离心率为
的离心率为 ,以椭圆
,以椭圆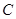 的左顶点
的左顶点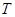 为
为
圆心作圆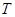 :
: ,设圆
,设圆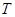 与椭圆
与椭圆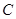 交于点
交于点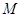 与点
与点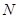 .
.
(1)求椭圆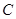 的方程;
的方程;
(2)求 的最小值,并求此时圆
的最小值,并求此时圆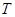 的方程;
的方程;
(3)设点 是椭圆
是椭圆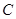 上异于
上异于 的任意一点,且直线
的任意一点,且直线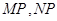 分别与
分别与 轴交于点
轴交于点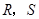 ,
,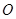 为坐标原点,求证:
为坐标原点,求证: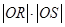 为定值.
为定值.
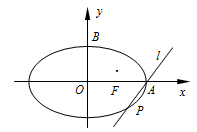
在平面直角坐标系 中,椭圆
中,椭圆 的右准线方程为
的右准线方程为 ,右顶点为
,右顶点为 ,
,
上顶点为 ,右焦点为
,右焦点为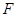 ,斜率为
,斜率为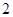 的直线
的直线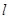 经过点
经过点 ,且点
,且点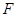 到直线
到直线 的距离为
的距离为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)将直线 绕点
绕点 旋转,它与椭圆
旋转,它与椭圆 相交于另一点
相交于另一点 ,当
,当 三点共线时,试确定直线
三点共线时,试确定直线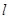 的斜率.
的斜率.
如图,在正方体 中,
中, 分别为
分别为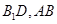 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证:平面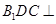 平面
平面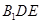 .
.
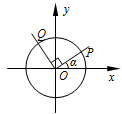
在平面直角坐标系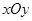 中,设锐角
中,设锐角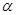 的始边与
的始边与 轴的非负半轴重合,终边与单位圆交于点
轴的非负半轴重合,终边与单位圆交于点 ,将射线
,将射线 绕坐标原点
绕坐标原点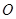 按逆时针方向旋转
按逆时针方向旋转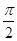 后与单位圆交于点
后与单位圆交于点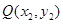 . 记
. 记 .
.
(1)求函数 的值域;
的值域;
(2)设 的角
的角 所对的边分别为
所对的边分别为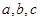 ,若
,若 ,且
,且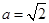 ,
, ,求
,求 .
.
设集合 ,
, 是
是 的两个非空子集,且满足集合
的两个非空子集,且满足集合 中的最大数小于集合
中的最大数小于集合 中的最小数,记满足条件的集合对
中的最小数,记满足条件的集合对 的个数为
的个数为 .
.
(1)求 的值;
的值;
(2)求 的表达式.
的表达式.
如图,在直三棱柱 中,
中, ,
, ,
, ,动点
,动点 满足
满足 ,当
,当 时,
时, .
.
(1)求棱 的长;
的长;
(2)若二面角 的大小为
的大小为 ,求
,求 的值..
的值..