(.(本小题满分12分)
已知点A,B的坐标分别是(0,–1),(0,1),直线AM,BM相交于点M,且它们的斜率之积为 .
.
(1)求点M的轨迹C的方程;
(2)若过点D(2,0)的直线l与(1)中的轨迹C交于不同的两点E、F (E在D、F之间),试求
(E在D、F之间),试求 与
与 面积之比的取值范围(O为坐标原点).
面积之比的取值范围(O为坐标原点).
((本小题满分12分)设函数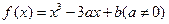 .
.
(1)若曲线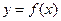 在点
在点 处与直线
处与直线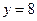 相切,求
相切,求 的值;
的值;
(2)求函数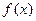 的单调区间与极值点.
的单调区间与极值点.
((本小题满分12分)已知抛物线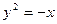 与直线
与直线 相交于
相交于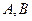 两点。
两点。
(1)求证:
(2)当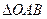 的面积等于
的面积等于 时,求
时,求 的值。
的值。
((本小题满分12分)设函数 的图象关于原点对称,且
的图象关于原点对称,且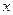 =1时,f(x)取极小值
=1时,f(x)取极小值 。
。
(1)求 的值;
的值;
(2)若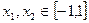 时,求证:
时,求证: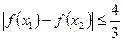 。
。
(本小题满分12分)已知双曲线的焦点在y轴上,两顶点间的 距离为4,渐近线方程为
距离为4,渐近线方程为
y=±2x.
(Ⅰ)求双曲线的标准方程;
(Ⅱ)设(Ⅰ)中双曲线的焦点F1,F2关于直线y=x的对称点分别为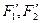 ,求以
,求以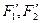
 为焦点,且过点P(0,2)的椭圆方程.
为焦点,且过点P(0,2)的椭圆方程.