某媒体对“男女同龄退佈”这一公众关注的问题进行了民意调査,右表是在某单位得到的数据(人数):
(I )能否有90%以上的把握认为对这一问题的看法与性别有关?
(II)进一步调查:
(i)从赞同“男女同龄退休” 16人中选出3人进行陈述发言,求事件“男士和女士各至少有1人发言”的概率;
(ii )从反对“男女同龄退休”的9人中选出3人进行座谈,设参加调査的女士人数为X,求X的分布列和均值.
附:
如图,设
是圆珠笔
上的动点,点
是
在
轴上的投影,
为
上一点,且
(Ⅰ)当
的在圆上运动时,求点
的轨迹
的方程;
(Ⅱ)求过点
且斜率为
的直线被
所截线段的长度.

叙述并证明余弦定理
(本小题满分14分)数列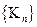 定义如下:
定义如下: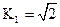 ,
,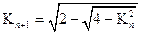 ,
,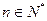 .
.
(1)求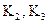 的值;
的值;
(2)求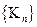 的通项;
的通项;
(3)若数列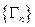 定义为:
定义为: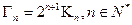 ,
,
①证明: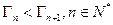 ;②证明:
;②证明: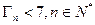 .
.
(本小题满分14分)已知函数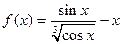
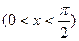 .
.
(1)求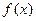 的导数
的导数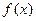 ;
;
(2)求证:不等式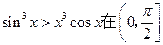 上恒成立;
上恒成立;
(3)求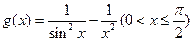 的最大值.
的最大值.
(本小题满分13分)已知抛物线C: 与直线l:
与直线l: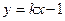 没有公共点,设点P为直线l上的动点,过P作抛物线C的两条切线,A,B为切点.
没有公共点,设点P为直线l上的动点,过P作抛物线C的两条切线,A,B为切点.
(1)证明:直线AB恒过定点Q;
(2)若点P与(1)中的定点Q的连线交抛物线C于M,N两点,证明: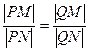 .
.