设函数 .
.
(I )讨论f(x)的单调性;
(II) ( i)若证明:当x>6时,
(ii)若方程f(x)=a有3个不同的实数解,求a的取值范围.
已知在锐角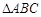 中,
中, 为角
为角 所对的边,且
所对的边,且 .
.
(1)求角 的值;
的值;
(2)若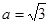 ,则求
,则求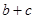 的取值范围.
的取值范围.
设等差数列 的前
的前 项和为
项和为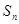 且
且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和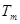 ,并求
,并求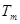 的最小值.
的最小值.
已知椭圆G: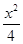 +y2=1.过
+y2=1.过 轴上的动点
轴上的动点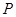 (m,0)作圆x2+y2=1的切线l交椭圆G于A,B两点.
(m,0)作圆x2+y2=1的切线l交椭圆G于A,B两点.
(1)求椭圆G上的点到直线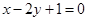 的最大距离;
的最大距离;
(2)①当实数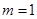 时,求A,B两点坐标;
时,求A,B两点坐标;
②将|AB|表示为m的函数,并求|AB|的最大值.
已知函数 (
( 是常数)在
是常数)在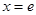 处的切线方程为
处的切线方程为 ,且
,且 .
.
(1)求常数 的值;
的值;
(2)若函数 (
( )在区间
)在区间 内不是单调函数,求实数
内不是单调函数,求实数 的取值范围.
的取值范围.
已知函数 的图象过点P(0,2),且在点M(-1,
的图象过点P(0,2),且在点M(-1, )处的切线方程
)处的切线方程 。
。
(1)求函数 的解析式;
的解析式;
(2)求函数 与
与 的图像有三个交点,求
的图像有三个交点,求 的取值范围。
的取值范围。