甲、乙两名同学在5次英语口语测试中的成绩统计如下面的茎叶图所示.
(1)现要从中选派一人参加英语口语竞赛,从统计学角度,你认为派哪位学生参加更合适,请说明理由;
(2)若将频率视为概率,对学生甲在今后的三次英语口语竞赛成绩进行预测,记这三次成绩中高于80分的次数为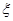 ,求
,求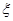 的分布列及数学期望
的分布列及数学期望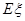 .
.
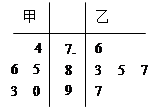
已知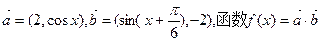 .
.
(1)求函数 的单调增区间;
的单调增区间;
(2)若 的值
的值
已知一条曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差都是1.
(1)求曲线C的方程;
(2)是否存在正数m, 对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有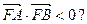 若存在,求出m的取值范围;若不存在,请说明理由。
若存在,求出m的取值范围;若不存在,请说明理由。
已知双曲线 的离心率为2,焦点到渐近线的距离为
的离心率为2,焦点到渐近线的距离为 ,点P的坐标为(0,-2),过P的直线l与双曲线C交于不同两点M、N.
,点P的坐标为(0,-2),过P的直线l与双曲线C交于不同两点M、N.
(1)求双曲线C的方程;
(2)设 (O为坐标原点),求t的取值范围
(O为坐标原点),求t的取值范围
若 P为椭圆 上任意一点,
上任意一点,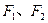 为左、右焦点,
为左、右焦点,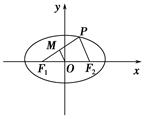
(1)若 的中点为M,求证:
的中点为M,求证: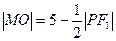 ;
;
(2)若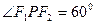 ,求
,求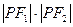 之值;
之值;
(3)椭圆上是否存在点P,使 ,若存在,求出P点的坐标,
,若存在,求出P点的坐标,
若不存在,请说明理由。
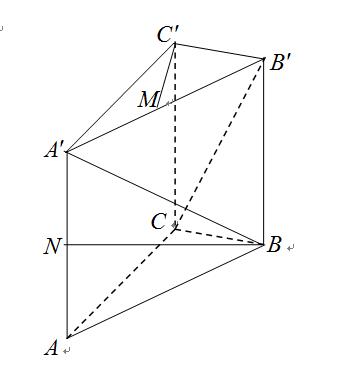
如图所示,直三棱柱 ,底面
,底面 中,
中, ,棱
,棱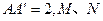 分别是
分别是 的中点.
的中点.
(1)求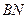 的长;
的长;
(2)求异面直线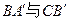 所成角的余弦值.
所成角的余弦值.