若 P为椭圆 上任意一点,
上任意一点,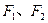 为左、右焦点,
为左、右焦点,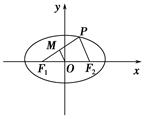
(1)若 的中点为M,求证:
的中点为M,求证: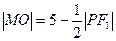 ;
;
(2)若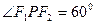 ,求
,求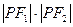 之值;
之值;
(3)椭圆上是否存在点P,使 ,若存在,求出P点的坐标,
,若存在,求出P点的坐标,
若不存在,请说明理由。
如图,在三棱锥 中,
中, ,
, ,
,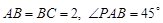 ,点
,点 、
、 、
、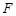 分别为
分别为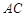 、
、 、
、 的中点.
的中点.
(1)求直线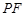 与平面
与平面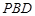 所成角的正弦值;
所成角的正弦值;
(2)求二面角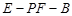 的大小.
的大小.
袋子 和
和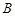 中装有若干个均匀的红球和白球,从
中装有若干个均匀的红球和白球,从 中摸出一个红球的概率是
中摸出一个红球的概率是 ,从
,从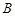 中摸出一个红球的概率为
中摸出一个红球的概率为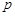 .
.
(1)从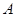 中有放回地摸球,每次摸出一个,共摸4次.
中有放回地摸球,每次摸出一个,共摸4次.
①恰好有2次摸到红球的概率;②第一次、第三次摸到红球的概率.
(2)若 、
、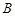 两个袋子中的球数之比为4,将
两个袋子中的球数之比为4,将 、
、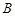 中的球装在一起后,从中摸出一个红球的概率是
中的球装在一起后,从中摸出一个红球的概率是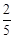 ,求
,求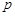 的值
的值
如图所示,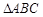 是正三角形,
是正三角形, 和
和 都垂直于平面
都垂直于平面 ,且
,且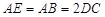 ,
,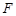 是
是 的中点.
的中点.
求证:(1)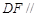 平面
平面 ;
;
(2) .
.
若 的展开式中只有第10项的二项式系数最大,
的展开式中只有第10项的二项式系数最大,
(1)求展开式中系数最大的项;
(2)设 ,求
,求 .
.
甲、乙两队在进行一场五局三胜制的排球比赛中,规定先赢三局的队获胜,并且比赛就此结束,现已知甲、乙两队每比赛一局,甲队获胜的概率为 ,乙队获胜的概率为
,乙队获胜的概率为 ,且每局比赛的胜负是相互独立的,问:
,且每局比赛的胜负是相互独立的,问:
(1)甲队以 获胜的概率是多少?
获胜的概率是多少?
(2)乙队获胜的概率是多少?